2021-2022學年江西省鷹潭市貴溪一中高二（下）期末數學試卷（理科）

一、選擇題：本題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項符合題目要求．

• 1．復數z=1+2i的共軛復數為

  z

  ，則|z²+

  z

  |=（　　）

  A． 2 2

  B． 2 5

  C．6

  D．8
  組卷：114引用：5難度：0.8

  解析

• 2．設集合A={x|x²-4≤0}，B={x|2x+a≤0}，且A∩B={x|-2≤x≤1}，則a=（　　）

  A．-4

  B．-2

  C．2

  D．4
  組卷：6404引用：57難度：0.8

  解析

• 3．已知

  a

  =

  （

  3

  4

  ）

  -

  2

  ，

  b

  =

  2

  3

  2

  ，

  c

  =

  （

  1

  3

  ）

  log

  3

  4

  9

  ，則a,b,c的大小關系為（　　）

  A．a＜b＜c

  B．a＜c＜b

  C．c＜a＜b

  D．c＜b＜a
  組卷：78引用：2難度：0.8

  解析

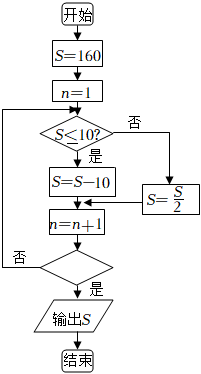• 4．執行如圖所示的程序框圖，若輸出的S=0，則空白判斷框中可填入的條件是（　　）

  A．n＞3？

  B．n＞4？

  C．n＞5？

  D．n＞6？
  組卷：11引用：3難度：0.8

  解析

• 5．已知sin（

  π

  12

  -

  α

  2

  ）=

  3

  3

  ，則sin（2α+

  π

  6

  ）的值為（　　）

  A．- 7 10

  B． 7 10

  C．- 7 9

  D． 7 9
  組卷：1081引用：6難度：0.5

  解析

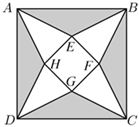• 6．如圖，正方形ABCD中灰色陰影部分為四個全等的等腰三角形，已知AB=2

  2

  ，EF=1，若在正方形ABCD內隨機取一點，則該點落在白色區域的概率為（　　）

  A． 1 2

  B． 5 8

  C． 9 16

  D． 2 3
  組卷：48引用：3難度：0.7

  解析

• 7．已知

  |

  b

  |

  =

  2

  2

  |

  a

  |

  =

  4

  ，當

  b

  ⊥

  （

  2

  a

  +

  b

  2

  ）

  時，向量

  a

  與

  b

  的夾角為（　　）

  A． π 4

  B． π 3

  C． 2 π 3

  D． 3 π 4
  組卷：58引用：1難度：0.7

  解析

三、解答題（共70分，解答應寫出文字說明、證明過程或演算步驟）

• 22．在平面直角坐標系xOy中，已知直線l的參數方程為

  x = - 1 + t

  y = 2 + t

  （t為參數），以坐標原點為極點，x軸正半軸為極軸建立極坐標系，曲線C的極坐標方程為ρ=-4cosθ．
  （1）求直線l的普通方程和曲線C的直角坐標方程；
  （2）設直線l與曲線C交于A，B兩點，若點P的坐標為（-1，2），求||PA|-|PB||．
  組卷：77引用：5難度：0.5

  解析

• 23．設函數f（x）=|2x-1|，g（x）=|ax+1|．
  （Ⅰ）求不等式f（x）≤1-x的解集；
  （Ⅱ）若不等式f（x）+g（x）≥2x在區間（

  1

  2

  ，1）上恒成立，求a的取值范圍．
  組卷：25引用：6難度：0.6

  解析