當前位置：試卷中心 > 試卷詳情

2023-2024學(xué)年山東省棗莊八中高二（上）第一次段考數(shù)學(xué)試卷

發(fā)布：2024/9/20 2:0:8

一、單項選擇題（本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一個選項是符合題目要求的）

1．過點（3，0）和點（4，
3
）的直線的傾斜角是（　　）
A．30° B．60° C．120° D．150°
組卷：71引用：15難度：0.9
解析
2．已知直線ax+by+2=0在y軸上的截距為-1，則b=（　　）
A．-2 B．-1 C．1 D．2
組卷：42引用：3難度：0.9
解析
3．已知直線ax+2y=0與直線x+（a+1）y+4=0平行，則實數(shù)a的值是（　　）
A．1 B．-2 C．1或-2 D．不存在
組卷：79引用：9難度：0.7
解析
4．已知空間向量
a
，
b
，
c
滿足
a
+
b
+
c
=
0
，
|
a
|
=
1
，
|
b
|
=
2
，
|
c
|
=
7
，則
a
與
b
的夾角為（　　）
A．30° B．45° C．60° D．90°
組卷：449引用：14難度：0.6
解析
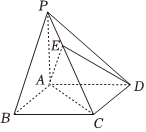5．如圖，四棱錐P-ABCD的底面ABCD為矩形，PA⊥平面ABCD，且EC=2PE，若
AE
=
x
AB
+
y
AD
+
z
AP
，則x+y+z=（　　）
A．
1
3
B．
2
3
C．1 D．
4
3
組卷：278引用：5難度：0.8
解析
6．已知直線l：（m+2）x+（m-1）y+m-1=0，若直線l與連接A（1，-2）、B（2，1）兩點的線段總有公共點，則直線l的傾斜角范圍為（　　）
A．
[
-
π
4
，
π
4
]
B．
[
3
π
4
，
π
）
C．
[
π
4
，
3
π
4
]
D．
[
0
，
π
4
]
∪
[
3
π
4
，
π
）
組卷：74引用：12難度：0.8
解析
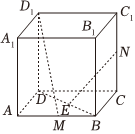7．如圖，在正方體ABCD-A₁B₁C₁D₁中，AB=1，M，N分別是棱AB，CC₁的中點，E是BD的中點，則異面直線D₁M，EN間的距離為（　　）?
A．
2
4
B．
2
2
C．1 D．
4
3
組卷：68引用：2難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內(nèi)容及下載

四、解答題（本大題共6個小題，共70分.除17題10分外，其余均為12分；解答應(yīng)寫出文字說明，證明過程或演算步驟）

21．空間中，兩兩互相垂直且有公共原點的三條數(shù)軸構(gòu)成直角坐標系，如果坐標系中有兩條坐標軸不垂直，那么這樣的坐標系稱為“斜坐標系”．現(xiàn)有一種空間斜坐標系，它任意兩條數(shù)軸的夾角均為60°，我們將這種坐標系稱為“斜60°坐標系”．我們類比空間直角坐標系，定義“空間斜60°坐標系”下向量的斜60°坐標：
i
，
j
，
k
分別為“斜60°坐標系”下三條數(shù)軸（x軸、y軸、z軸）正方向的單位向量，若向量
n
=
x
i
+
y
j
+
z
k
，則
n
與有序?qū)崝?shù)組（x,y,z）相對應(yīng)，稱向量
n
的斜60°坐標為[x,y,z]，記作
n
=
[
x
,
y
,
z
]
．
（1）若
a
=
1
，
2
，
3
，
b
=
[
-
1
，
1
，
2
]
，求
a
+
b
的斜60°坐標；
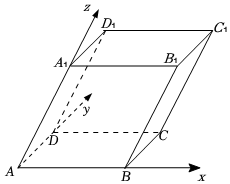
（2）在平行六面體ABCD-ABC₁D₁中，AB=AD=2，AA₁=3，∠BAD=∠BAA₁=∠DAA₁=60°，如圖，以
{
AB
，
AD
，
A
A
1
}
為基底建立“空間斜60°坐標系”．
①若
BE
=
EB
1
，求向量
ED
1
的斜60°坐標；
②若
AM
=
[
2
，
t
,
0
]
，且
AM
⊥
A
C
1
，求
|
AM
|
．
組卷：289引用：12難度：0.6
解析
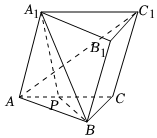22．已知三棱柱ABC-A₁B₁C₁中，AC=AA₁=4，BC=2，∠ACB=90°，A₁B⊥AC₁．
（1）求證：平面A₁ACC₁⊥平面ABC；
（2）若∠A₁AC=60°，在線段AC上是否存在一點P使平面BA₁P和平面A₁ACC₁所成角的余弦值為
3
4
？若存在，確定點P的位置；若不存在，說明理由．
組卷：740引用：16難度：0.6
解析