2023-2024學年天津二十中高三（上）期中數學試卷

一、單選題（本大題共10小題，共50分.在每小題列出的選項中，選出符合題目的一項）

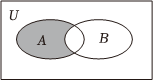• 1．已知全集U=R，集合A={0，1，2，3，4，5，6}，B={x|

  x

  3

  -

  x

  ≤0}，則圖中陰影部分表示的集合為（　　）

  A．{1，2}

  B．{0，1，2}

  C．{1，2，3}

  D．{0，1，2，3}
  組卷：246引用：4難度：0.8

  解析

• 2．設a,b是平面α內兩條不同的直線，l是平面α外的一條直線，則“l⊥a,l⊥b”是“l⊥α”的（　　）

  A．充要條件

  B．充分而不必要的條件

  C．必要而不充分的條件

  D．既不充分也不必要的條件
  組卷：152引用：52難度：0.9

  解析

• 3．函數y=

  sin

  2

  x

  1

  +

  cosx

  的部分圖象大致為（　　）

  A．

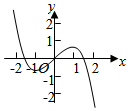
  B．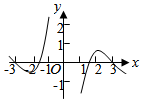

  C．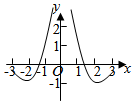

  D．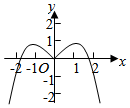
  組卷：119引用：8難度：0.7

  解析

• 4．已知a=log_1.40.7，b=1.4^0.7，c=0.7^1.4，則a,b,c的大小關系是（　　）

  A．a＜b＜c

  B．a＜c＜b

  C．c＜a＜b

  D．c＜b＜a
  組卷：295引用：4難度：0.8

  解析

• 5．《萊茵德紙草書》（RhindPapyrus）是世界上最古老的數學著作之一，書中有這樣一道題目：把93個面包分給5個人，使每個人所得面包個數成等比數列，且使較小的兩份面包個數之和等于中間一份面包個數的四分之三，則中間一份面包的個數為（　　）

  A．8

  B．12

  C．16

  D．20
  組卷：179引用：4難度：0.8

  解析

• 6．已知

  sin

  （

  x

  +

  π

  12

  ）

  =

  -

  1

  4

  ，則

  cos

  （

  5

  π

  6

  -

  2

  x

  ）

  =（　　）

  A． 7 8

  B． 1 8

  C． - 7 8

  D． - 1 8
  組卷：293引用：4難度：0.5

  解析

• 7．將函數

  f

  （

  x

  ）

  =

  2

  sinxcosx

  +

  3

  cos

  2

  x

  的圖象向右平移

  π

  3

  個單位，得到g（x）的圖象，再將g（x）圖象上的所有點的橫坐標變成原來的

  1

  2

  ，得到h（x）的圖象，則下列說法正確的個數是（　　）
  ①函數h（x）的最小正周期為2π；
  ②

  （

  π

  3

  ，

  0

  ）

  是函數h（x）圖象的一個對稱中心；
  ③函數h（x）圖象的一個對稱軸方程為

  x

  =

  5

  π

  6

  ；
  ④函數h（x）在區間

  [

  -

  π

  24

  ，

  5

  π

  24

  ]

  上單調遞增

  A．1

  B．2

  C．3

  D．4
  組卷：966引用：7難度：0.5

  解析

三、解答題（本大題共4小題，共60分.解答應寫出文字說明，證明過程或演算步驟）

• 21．已知等差數列{a_n}的前n項和為S_n，a₁=1，S₄=10，數列{b_n}滿足：b₁=3，

  b

  n

  +

  1

  =

  2

  b

  n

  -

  1

  （

  n

  ∈

  N

  *

  ）

  ．
  （1）證明：{b_n-1}是等比數列；
  （2）證明：S_2n+1?b_n＞2S_n?b_n+1；
  （3）設數列{c_n}滿足：

  c

  n

  =

  a n + 1 a 2 n a 2 n + 2 ， n 為奇數

  a 2 n b n ， n 為偶數

  ．證明：

  2

  n

  ∑

  k

  =

  1

  c

  k

  ＜

  9

  4

  ．
  組卷：710引用：4難度：0.4

  解析

• 22．已知函數f（x）=axe^1-x與g（x）=

  2

  x

  x

  2

  +

  1

  有相同的最大值（其中e為自然對數的底數）．
  （1）求實數a的值；
  （2）證明：?x∈[0，1]，都有f（x）≥g（x）；
  （3）若直線y=m（m∈R）與曲線y=f（x）有兩個不同的交點A（x₁，y₁），B（x₂，y₂），求證：x₁+x₂＜

  2

  m

  ．
  組卷：78引用：3難度：0.3

  解析