2012-2013學年北京市十一學校高三（上）暑期檢測數學試卷1（文科）

一、選擇題：本大題共8小題，每小題5分，共40分．

• 1．若全集U=R，A={x|0＜x＜2}，B=x||x|≤1}，則（?_UA）∩B為（　　）

  A．{x|-1≤x＜0}

  B．{x|-1≤x≤1}

  C．{x|1≤x≤2}

  D．{x|-1≤x≤0}
  組卷：4引用：2難度：0.9

  解析

• 2．函數

  f

  （

  x

  ）

  =

  x

  +

  4

  +

  lo

  g

  2

  （

  6

  -

  2

  x

  ）

  的定義域是（　　）

  A．{x|x＞3}

  B．{x|-4＜x＜3}

  C．{x|x＞-4}

  D．{x|-4≤x＜3}
  組卷：255引用：5難度：0.9

  解析

• 3．命題“?x∈R，使x＞1”的否定是（　　）

  A．?x∈R，都有x＞1	B．?x∈R，使x＜1
  C．?x∈R，都有x≤1	D．?x∈R，使x≤1
  組卷：127引用：2難度：0.9

  解析

• 4．函數f（x）的圖象如圖所示，下列數值排序正確的是（　　）
  

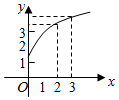
  A．0＜f′（2）＜f′（3）＜f（3）-f（2）

  B．0＜f′（3）＜f（3）-f（2）＜f′（2）

  C．0＜f（3）＜f′（2）＜f（3）-f（2）

  D．0＜f（3）-f（2）＜f′（2）＜f′（3）
  組卷：312引用：30難度：0.7

  解析

• 5．函數

  f

  （

  x

  ）

  =

  （

  1

  2

  ）

  x

  -sinx在區間[0，2π]上的零點個數為（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：247引用：44難度：0.9

  解析

• 6．在△ABC中，AC=

  7

  ，BC=2，B=60°，則BC邊上的高等于（　　）

  A． 3 2

  B． 3 3 2

  C． 3 + 6 2

  D． 3 + 39 4
  組卷：1973引用：39難度：0.9

  解析

三、解答題：（本大題共6個小題，共80分，）

• 19．定義：兩個連續函數（圖象不間斷）f（x），g（x）在區間[a,b]上都有意義，我們稱函數|f（x）+g（x）|在[a,b]上的最大值叫做函數f（x）與g（x）在區間[a,b]上的“絕對和”．
  （1）試求函數f（x）=x²與g（x）=x（x+2）（x-4）在閉區間[-2，2]上的“絕對和”．
  （2）設h_m（x）=-4x+m及f（x）=x²都是定義在閉區間[1，3]上，記h_m（x）與f（x）的“絕對和”為D_m，如果D（m）的最小值是D（m₀），則稱f（x）可用

  h

  m

  0

  （

  x

  ）

  “替代”，試求m₀的值，使f（x）可用

  h

  m

  0

  （

  x

  ）

  “替代”．
  組卷：16引用：5難度：0.1

  解析

• 20．已知函數f（x）=（ax²+bx+c）e^x在[0，1]上單調遞減且滿足f（0）=1，f（1）=0．
  （1）求a取值范圍；
  （2）設g（x）=f（x）-f′（x），求g（x）在[0，1]上的最大值和最小值．
  組卷：1201引用：11難度：0.1

  解析