2022-2023學年江蘇省揚州市江都實驗中學八年級（上）第一次質檢數學試卷
發布：2024/4/20 14:35:0
一、選擇題（本大題共有8小題，每小題3分，共24分．在每小題所給出的四個選項中，恰有一項是符合題目要求的，請將正確選項前的字母填涂在答題卡相應位置上）
-
1．下列倡導節約的圖案中是軸對稱圖形的是（ ）
組卷：355引用：27難度：0.9 -
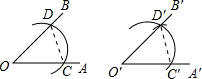2．用直尺和圓規作一個角等于已知角的示意圖如圖，則說明∠D′O′C′=∠DOC的依據是（ ）組卷：1181引用：10難度：0.9 -
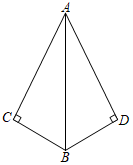3．如圖，∠C=∠D=90°，添加下列條件：①AC=AD；②∠ABC=∠ABD；③BC=BD，其中能判定Rt△ABC與Rt△ABD全等的條件的個數是（ ）組卷：1428引用：12難度：0.7 -
4．若等腰三角形的一個角為50°，則其他兩個角的度數為（ ）
組卷：357引用：2難度：0.7 -
5．如圖，若△ABC和△DEF的面積分別為S1、S2，則（ ）組卷：3464引用：81難度：0.9 -
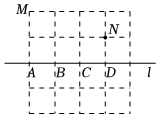6．如圖，在正方形網格中有M，N兩點，在直線l上求一點P使PM+PN最短，則點P應選在（ ）組卷：2467引用：25難度：0.7 -
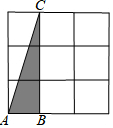7．如圖，在3×3的正方形網格中，格線的交點稱為格點，以格點為頂點的三角形稱為格點三角形，圖中的△ABC為格點三角形，在圖中與△ABC成軸對稱的格點三角形可以畫出（ ）組卷：1972引用：16難度：0.6 -
8．規定：從三角形（不是等腰三角形）一個頂點引出一條射線與對邊相交，頂點與交點之間的線段把這個三角形分割成兩個小三角形，如果分得的兩個小三角形中一個為等腰三角形，另一個與原來三角形三個角都相等，我們把這條線段叫做這個三角形的“等角分割線”．在△ABC中，∠A=42°，CD是△ABC的等角分割線，則∠ACB的度數不可能是（ ）
組卷：176引用：1難度：0.5
二、填空題（本大題共有10小題，每小題3分，共30分．不需寫出解答過程，請把答案直接填寫在答題卡相應位置上）
-
9．已知實數x,y滿足|x-2|+（y-4）2=0，則以x,y的值為兩邊長的等腰三角形的周長是 ．
組卷：77引用：2難度：0.7
三、解答題（本大題共有10小題，共96分．請在答題卡指定區域內作答，解答時應寫出必要的文字說明、證明過程或演算步驟）
-
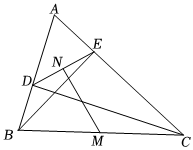27．如圖，已知銳角△ABC中，CD、BE分別是AB、AC邊上的高，M、N分別是線段BC、DE的中點．
（1）求證：MN⊥DE；
（2）若∠ABC=70°，∠ACB=50°，連結DM、ME，求∠DME的度數；
（3）猜想∠DME與∠A之間的關系，并證明你的猜想．組卷：589引用：3難度：0.6 -
28．【閱讀理解】
（1）如圖，已知△ABC中，AB=AC，點D、E是邊BC上兩動點，且滿足∠DAE=∠BAC，12
求證：BD+CE＞DE．
我們把這種模型稱為“半角模型”，在解決“半角模型”問題時，旋轉是一種常用的方法．
小明的解題思路：將半角∠DAE兩邊的三角形通過旋轉，在一邊合并成新的△AFE，然后證明與半角形成的△ADE全等，再通過全等的性質進行等量代換，得到線段之間的數量關系．
請你根據小明的思路寫出完整的解答過程．
證明：將△ABD繞點A旋轉至△ACF，使AB與AC重合，連接EF，
……
【應用提升】
（2）如圖，正方形ABCD（四邊相等，四個角都是直角）的邊長為4，點P從點A出發，以每秒1個單位長度的速度沿射線AD向點D運動；點Q從點D同時出發，以相同的速度沿射線AD方向向右運動，當點P到達點D時，點Q也停止運動，連接BP，過點P作BP的垂線交過點Q平行于CD的直線l于點E，BE于CD相交于點F，連接PF，設點P運動時間為t（s），
①求∠PBE的度數；
②試探索在運動過程中△PDF的周長是否隨時間t的變化而變化？若變化，說明理由；若不變，試求這個定值．組卷：730引用：3難度：0.1