當前位置：試卷中心 > 試卷詳情

2022年貴州省遵義市紅花崗區中考數學三模試卷

發布：2024/4/20 14:35:0

一、選擇題：（本題共12小題，每小題4分，共48分.在每小題給出的四個選項中，只有一項是符合題目要求的，請用2B鉛筆把答題卡上對應題目的答案標號涂黑、涂滿）

1．比-2022小的數是（　　）
A．2021 B．0 C．-2023 D．-1
組卷：198引用：4難度：0.9
解析
2．2022年4月，上海疫情嚴重，全國各省分赴支援．遵義人民也緊急運輸50000千克蔬菜支援，將數據50000用科學記數法表示為（　　）
A．0.5×10⁷ B．5×10⁶ C．5×10⁵ D．5×10⁴
組卷：25引用：3難度：0.7
解析
3．分別觀察如圖所示幾何體，其中主視圖、左視圖和俯視圖完全相同的有（　　）
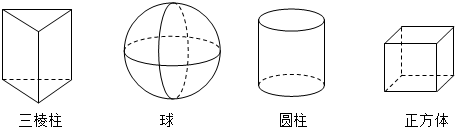
A．1個 B．2個 C．3個 D．4個
組卷：171引用：2難度：0.8
解析
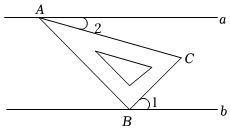4．如圖，30°的直角三角板的頂點A、B分別在直線a,b上．若a∥b,∠1=45°，則∠2的度數為（　　）
A．10° B．15° C．20° D．25°
組卷：113引用：2難度：0.8
解析
5．下列各式中計算結果為x⁴的是（　　）
A．x²+x² B．x⁸-x⁶ C．x⁶÷x² D．x?x⁴
組卷：88引用：1難度：0.7
解析
6．若關于x的一元二次方程x²-4x+k=0有兩個不相等的實數根，則k的值可以是（　　）
A．3 B．4 C．5 D．6
組卷：109引用：6難度：0.7
解析
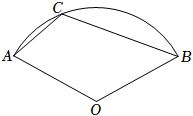7．如圖，C是⊙O劣弧AB上一點，OA=2，∠ACB=120°．則劣弧AB的長度為（　　）
A．
1
3
π B．
2
3
π C．
4
3
π D．
8
3
π
組卷：573引用：2難度：0.6
解析
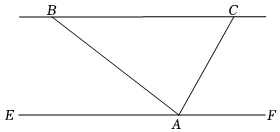8．如圖，小明為了測量遵義市湘江河的對岸邊上B，C兩點間的距離，在河的岸邊與BC平行的直線EF上點A處測得∠EAB=37°，∠FAC=60°，已知河寬30米，則B，C兩點間的距離為（　　）（參考數據：sin37°≈
3
5
，cos37°≈
4
5
，tan37°≈
3
4
）
A．（18+25
3
）米 B．（40+10
3
）米 C．（24+10
3
）米 D．（40+30
3
）米
組卷：327引用：1難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題：（本題共8小題，共86分.答題請用0.5毫米黑色墨水簽字筆或鋼筆書寫在答題卡的相應位置上.解答是應寫出必要的文字說明，證明過程或演算步驟.）

23．實踐活動
（1）數學活動一：
寬與長的比是
5
-
1
2
的矩形叫做黃金矩形，黃金矩形給我們以協調、勻稱的美感，世界各國許多著名的建筑，都采用了黃金矩形的設計．在數學活動課上，小紅按如下步驟折疊出一個矩形：
第一步，在一張矩形紙片的-端，利用圖①的方法折出一個正方形ABCD，然后把紙片展平；
第二步，如圖②把這個正方形ABCD對折成兩個完全重合的矩形，再把紙片展平；
第三步，如圖③，折出內側矩形EFBC的對角線CF，并把CF折到圖中所示FN處；
第四步，如圖④，展平紙片，按照點N折出NM，得到矩形BNMC．
若AD=2，請證明矩形BNMC是黃金矩形．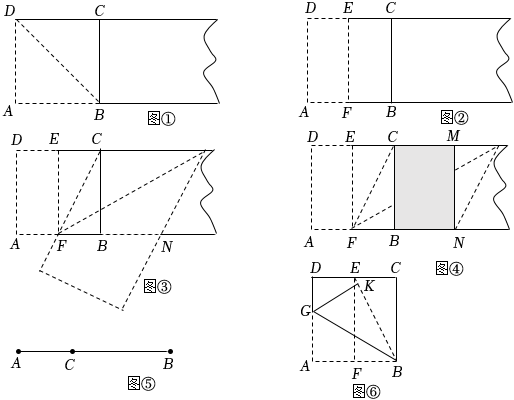

（2）數學活動二：
如圖⑤，點C在線段AB上，且滿足AC：BC=BC；AB，即BC²=AC?AB，此時，我們說點C是線段AB的黃金分割點，且通過計算可得
BC
AB
=
5
-
1
2
．小紅發現還可以從活動一的第三步開始修改折疊方式，如圖⑥，折出右側矩形EFBC的對角線EB，把AB邊沿BG折疊，使得A點落在對角線BE上的K點處，若AD=2，請通過計算說明G點是AD的黃金分割點．
組卷：105引用：1難度：0.3
解析
24．如圖（1），△ABC中，AC=BC=6，∠C=90°，點P在線段AC上，從C點向A點運動，∠PBE=90°，BP=BE，PE交BC于點D，完成下列問題：
（1）①點E到BC邊的距離為
；
②若CD=x,△BDE的面積為S，則S與x的函數關系式為
；（不寫自變量取值范圍）
（2）當△BDE的面積為15時，若PC＜
1
2
AC，以C為原點，AC、BC所在直線分別為x、y軸建立坐標系如圖（2），拋物線C₁過點A、D、B；
①點Q在拋物線C₁上，且位于線段PB的下方，過點Q作QN⊥PB，垂足為點N，是否存在點Q，使得QN最長，若存在，請求出QN的長度和Q點坐標；若不存在，請說明理由；
②將拋物線C₁繞原點C旋轉180°，得到拋物線C₂，當-2a≤x≤-a時（a＞0），拋物線C₂有最大值2a,求a值．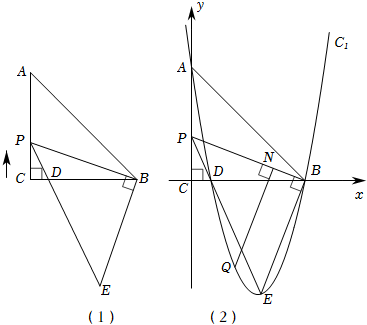
組卷：125引用：1難度：0.1
解析