2023年天津市十二區重點學校高考數學二模試卷

一、選擇題：本題共9小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合A={x|x＜5}，B={x|x²-8x+7＜0}，則（?_RA）∩B=（　　）

  A．{x|5≤x≤7}

  B．{x|5≤x＜7}

  C．{x|5＜x≤7}

  D．{x|5＜x＜7}
  組卷：259引用：3難度：0.8

  解析

• 2．已知a≠0，命題p：x=1是一元二次方程ax²+bx+c=0的一個根，命題q：a+b+c=0，則p是q的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：420引用：5難度：0.7

  解析

• 3．函數y=xcosx+sinx在區間[-π，π]上的圖象可能是（　　）

  A．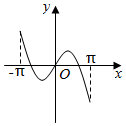

  B．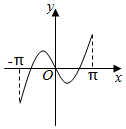

  C．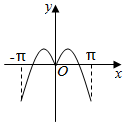

  D．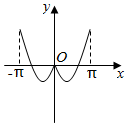
  組卷：4505引用：43難度：0.7

  解析

• 4．某學校組建了演講，舞蹈，航模，合唱，機器人五個社團，全校所有學生每人都參加且只參加其中一個社團，校團委在全校學生中隨機選取一部分學生（這部分學生人數少于全校學生人數）進行調查，并將調查結果繪制了如圖不完整的兩個統計圖，則（　　）
  

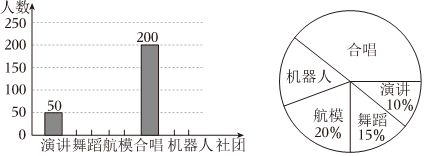
  A．選取的這部分學生的總人數為1000人

  B．選取的學生中參加機器人社團的學生數為80人

  C．合唱社團的人數占樣本總量的40%

  D．選取的學生中參加合唱社團的人數是參加機器人社團人數的2倍
  組卷：262引用：3難度：0.6

  解析

• 5．設函數f（x）=log₂|x|，若a=f（log

  1

  3

  2），b=f（log₅2），c=f（e^0.2），則a,b,c的大小為（　　）

  A．b＜a＜c

  B．c＜a＜b

  C．b＜c＜a

  D．a＜b＜c
  組卷：859引用：12難度：0.7

  解析

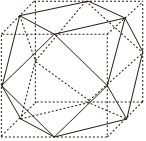• 6．“阿基米德多面體”被稱為半正多面體（semi-regularsolid），是由邊數不全相同的正多邊形為面圍成的多面體，它體現了數學的對稱美．如圖所示，將正方體沿交于一頂點的三條棱的中點截去一個三棱錐，共可截去八個三棱錐，得到八個面為正三角形、六個面為正方形的一種半正多面體．已知正方體棱長為6，則該半正多面體外接球的表面積為（　　）

  A．48π

  B．56π

  C．64π

  D．72π
  組卷：627引用：3難度：0.5

  解析

三、解答題（本大題5小題，共75分.解答應寫出必要的文字說明，證明過程或演算步驟）

• 19．已知數列{a_n}滿足：

  2

  a

  n

  +

  1

  =

  a

  n

  +

  a

  n

  +

  2

  （

  ?

  n

  ∈

  N

  *

  ）

  ，正項數列{b_n}滿足：

  b

  2

  n

  +

  1

  =

  b

  n

  ?

  b

  n

  +

  2

  （

  ?

  n

  ∈

  N

  *

  ）

  ，且2a₁=b₁=2，a₄=b₂，b₅=4b₃．
  （1）求{a_n}，{b_n}的通項公式；
  （2）已知

  c

  n

  =

  a 2 n - 1 ， n 為奇數

  （ 3 a n - 2 ） b n - 2 （ b n + 1 ） （ b n + 2 + 1 ） ， n 為偶數

  ，求：

  2

  n

  +

  1

  ∑

  k

  =

  1

  c

  k

  ；
  （3）求證：

  1

  a

  3

  1

  +

  1

  a

  3

  2

  +

  1

  a

  3

  3

  +

  …

  +

  1

  a

  3

  n

  ＜

  5

  4

  ．
  組卷：1296引用：5難度：0.5

  解析

• 20．已知函數

  f

  （

  x

  ）

  =

  e

  x

  -

  lnx

  x

  -

  1

  ．
  （1）求曲線y=f（x）在點（1，f（1））處的切線方程；
  （2）若函數

  g

  （

  x

  ）

  =

  f

  （

  x

  ）

  -

  a

  x

  有兩個零點x₁，x₂（其中x₁＜x₂）．
  （i）求實數a的取值范圍；
  （ii）若存在實數n,當n≤3時，使不等式

  m

  ＜

  x

  1

  e

  x

  1

  +

  n

  x

  2

  e

  x

  2

  恒成立，求實數m的取值范圍．
  組卷：377引用：2難度：0.5

  解析