當前位置：試卷中心 > 試卷詳情

2021-2022學年湖南省長沙實驗中學高一（下）入學數學試卷

發布：2024/11/21 4:0:1

一、單選題（本題共8小題，每小題5分。在每小題給出的四個選項中，只有一項是符合題目要求的。）

1．設集合A={x|-1＜x≤0}，
B
=
{
x
|
x
＞
-
1
2
}
，則A∩B=（　　）
A．（
-
1
2
，0） B．（
-
1
2
，0] C．[-1，+∞） D．（-1，+∞）
組卷：49引用：1難度：0.8
解析
2．已知命題p：“?x∈R，x²-x+1＜0”，則￢p為（　　）
A．?x∈R，x²-x+1≥0 B．?x?R，x²-x+1≥0
C．?x∈R，x²-x+1≥0 D．?x∈R，x²-x+1＜0
組卷：245引用：15難度：0.9
解析
3．函數f（x）=lgx+x-4的零點為x₀，x₀∈（k,k+1）（k∈Z），則k的值為（　　）
A．1 B．2 C．3 D．4
組卷：82引用：2難度：0.7
解析
4．函數f（x）=log₂|x|+cosx的大致圖象是（　　）
A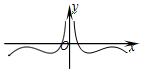． B． C． D．
組卷：110引用：4難度：0.8
解析
5．若
sin
（
θ
-
π
3
）
=
2
3
，則
cos
（
θ
+
π
6
）
=（　　）
A．
-
2
3
B．
2
3
C．
2
3
D．
-
2
3
組卷：487引用：2難度：0.8
解析
6．若0＜a＜1，b＞0，且a^b-a^-b=-2，則a^b+a^-b的值為（　　）
A．
2
2
B．
±
2
2
C．
-
2
2
D．
6
組卷：456引用：3難度：0.8
解析
7．若函數f（x）=cos（2x-
π
4
）-a（x∈[0，
9
π
8
]）恰有三個不同的零點x₁，x₂，x₃，則x₁+x₂+x₃的取值范圍是（　　）
A．[
5
π
4
，
11
π
8
） B．[
9
π
4
，
7
π
2
） C．（
5
π
4
，
11
π
8
] D．（
9
π
4
，
7
π
2
]
組卷：176引用：2難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（本題共6小題，17題10分，18-22題每題12分，解答題應寫出必要的文字說明，證明過程或演算步驟）

21．2011年六月康菲公司由于機器故障，引起嚴重的石油泄漏，造成了海洋的巨大污染，某沿海漁場也受到污染．為降低污染，漁場迅速切斷與海水聯系，并決定在漁場中投放一種可與石油發生化學反應的藥劑．已知每投放a（1≤a≤4，且a∈R）個單位的藥劑，它在水中釋放的濃度y（克/升）隨著時間x（天）變化的函數關系式近似于y=af（x），其中f（x）=
16
8
-
x
-
1
（
0
≤
x
≤
4
）
5
-
1
2
x
（
4
＜
x
≤
10
）
，若多次投放，則某一時刻水中的藥劑濃度為每次投放的藥劑在相應時刻所釋放的濃度之和．根據實驗，當水中藥劑的濃度不低于4（克/升）時，它才能起到有效治污的作用．稱為有效凈化；當藥劑在水中釋放的濃度不低于6（毫克/升）且不高于18（毫克/升）時稱為最佳凈化．
（Ⅰ）若一次投放4個單位的藥劑，則有效治污時間可達幾天？
（Ⅱ）若第一次投放2個單位的藥劑，6天后再投放a個單位的藥劑，要使接下來的4天中能夠持續有效治污，試問a的最小值（精確到0.1，參考數據：
2
取1.4）．
組卷：163引用：3難度：0.3
解析
22．已知函數f（x）的定義域為D，若恰好存在n個不同的實數x₁，x₂，…，x_n∈D，使得f（-x_i）=-f（x_i）（其中i=1，2，…，n,n∈N^*），則稱函數f（x）為“n級J函數”．
（1）若函數f（x）=x²-1，試判斷函數f（x）是否為“n級J函數”，如果是，求出n的值，如果不是，請說明理由；
（2）若函數f（x）=2cosωx+1，x∈[-2π，2π]是“2022級J函數”，求正實數ω的取值范圍；
（3）若函數
f
（
x
）
=
4
x
-
（
m
+
2
）
?
2
x
+
m
2
4
是定義在R上的“4級J函數”，求實數m的取值范圍．
組卷：118引用：2難度：0.3
解析