2021-2022學(xué)年浙江省紹興市高二（下）期末數(shù)學(xué)試卷

一、單項選擇題（本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．設(shè)集合A={x|x≥0}，B={x|-1＜x＜2}，則A∩B=（　　）

  A．{x|-1＜x＜0}

  B．{x|0≤x＜2}

  C．{x|x＞-1}

  D．{x|x≥0}
  組卷：99引用：1難度：0.8

  解析

• 2．若復(fù)數(shù)z滿足zi=1-i（i為虛數(shù)單位），則復(fù)數(shù)z等于（　　）

  A．1+i

  B．-1-i

  C．1-i

  D．-1+i
  組卷：11引用：3難度：0.9

  解析

• 3．命題“?n∈N，n²＞2ⁿ”的否定為（　　）

  A．?n∈N，n2＞2n

  B．?n∈N，n2≤2n

  C．?n∈N，n2≤2n

  D．?n?N，n2≤2n
  組卷：123引用：4難度：0.8

  解析

• 4．已知△ABC中，“sinA＞

  1

  2

  ”是“A＞

  π

  6

  ”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：80引用：6難度：0.9

  解析

• 5．在同一直角坐標(biāo)系中，函數(shù)y=a^-x，y=x^a（a＞0，且a≠1）的圖象可能是（　　）

  A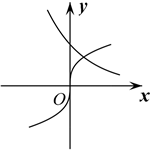．	B．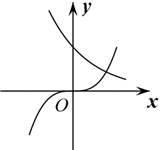
  C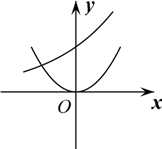．	D．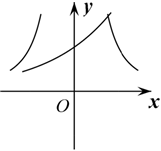
  組卷：114引用：2難度：0.6

  解析

• 6．從5名男生2名女生中任選3人參加學(xué)校組織的“喜迎二十大，奮進新征程”的演講比賽，則在男生甲被選中的條件下，男生乙和女生丙至少一人被選中的概率是（　　）

  A． 1 2

  B． 4 7

  C． 3 5

  D． 2 3
  組卷：133引用：2難度：0.8

  解析

• 7．已知平面向量

  a

  ，

  b

  ，滿足

  |

  a

  |

  =

  1

  ，且對任意實數(shù)λ，有

  |

  b

  -

  λ

  a

  |

  ≥

  1

  ，設(shè)

  b

  與

  b

  -

  a

  夾角為θ，則cosθ的取值范圍是（　　）

  A． （ 0 ， 2 2 ]

  B． （ 0 ， 3 5 ]

  C． [ 2 2 ， 1 ）

  D． [ 3 5 ， 1 ）
  組卷：96引用：2難度：0.6

  解析

四、解答題（本大題共6小題，共70分，解答應(yīng)寫出文字說明、證明過程或演算步驟）

• 21．某市為篩查新冠病毒，需要檢驗核酸樣本是否為陽性，現(xiàn)有k（k∈N^*且k≥2）份核酸樣本，可采用以下兩種檢驗方式：①逐份檢驗：對k份樣本逐份檢驗，需要檢驗k次；②混合檢驗：將k份樣本混合在一起檢驗，若檢驗結(jié)果為陰性，則k份樣本全為陰性，因而這k份樣本只需檢驗1次；若檢驗結(jié)果為陽性，為了確定其中的陽性樣本，就需重新采集核酸樣本后再對這k份新樣本進行逐份檢驗，此時檢驗總次數(shù)為k+1次．假設(shè)在接受檢驗的核酸樣本中，每份樣本的檢驗結(jié)果是相互獨立的，且每份樣本結(jié)果為陽性的概率是p（0＜p＜1）．
  （1）若對k份樣本采用逐份檢驗的方式，求恰好經(jīng)過4次檢驗就檢驗出2份陽性的概率（結(jié)果用p表示）；
  （2）若k=20，設(shè)采用逐份檢驗的方式所需的檢驗次數(shù)為X，采用混合檢驗的方式所需的檢驗次數(shù)為Y，試比較E（X）與E（Y）的大小．
  組卷：75引用：1難度：0.5

  解析

• 22．已知函數(shù)f（x）=（x-a）ln（x+1）+（a-1）x+a,x∈[0，2]，a∈R．
  （1）若a=1，求f（x）在點P（1，f（1））處的切線方程；
  （2）若f（x）≤0恒成立，求a的取值范圍．
  組卷：82引用：1難度：0.3

  解析