2022-2023學年廣東省東莞市光明中學八年級（下）期中數學試卷

一、選擇題（共10小題，每小題3分，共30分）

• 1．下列根式中的最簡二次根式是（　　）

  A． 7

  B． 8

  C． 1 4

  D． m 2
  組卷：645引用：11難度：0.7

  解析

• 2．下列幾組數中，能作為直角三角形三邊長度的是（　　）

  A．1，1， 3

  B．3，4，5

  C．2，3，4

  D．5，7，9
  組卷：164引用：7難度：0.6

  解析

• 3．在?ABCD中，∠C=32°，則∠A的度數為（　　）

  A．148°

  B．128°

  C．138°

  D．32°
  組卷：265引用：3難度：0.9

  解析

• 4．二次根式

  1

  x

  -

  2

  有意義，則x滿足的條件是（　　）

  A．x＜2

  B．x＞2

  C．x≥2

  D．x≤2
  組卷：2008引用：13難度：0.7

  解析

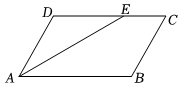• 5．如圖，在平行四邊形ABCD中，AE平分∠BAD，交CD邊于點E，AD=6，EC=4，則AB長為（　　）

  A．4

  B．6

  C．10

  D．12
  組卷：390引用：2難度：0.5

  解析

• 6．下列曲線中表示y是x的函數的是（　　）

  A．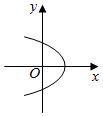

  B．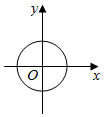

  C．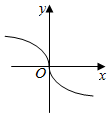

  D．
  組卷：3330引用：37難度：0.6

  解析

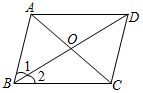• 7．如圖，要使?ABCD成為矩形，需添加的條件是（　　）

  A．AB=BC

  B．∠ABC=90°

  C．AC⊥BD

  D．∠1=∠2
  組卷：946引用：7難度：0.5

  解析

五、解答題（共2小題，每小題12分，共24分）

• 22．如圖1，已知四邊形ABCD是正方形，E是對角線BD上的一點，連接AE，CE．
  （1）求證：AE=CE；
  （2）如圖2，點P是邊CD上的一點，且PE⊥BD于E，連接BP，O為BP的中點，連接EO．若∠PBC=30°，求∠POE的度數；
  （3）在（2）的條件下，若OE=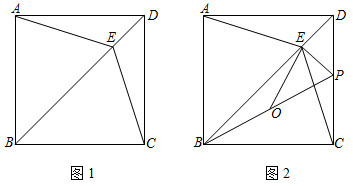

  2

  ，求CE的長．
  
  組卷：1214引用：11難度：0.3

  解析

• 23．如圖，在Rt△ABC中，∠B=90°，AB=5，∠C=30°．點D從點C出發沿CA方向以每秒2個單位長的速度向點A勻速運動，同時點E從點A出發沿AB方向以每秒1個單位長的速度向點B勻速運動，當其中一個點到達終點時，另一個點也隨之停止運動．設點D、E運動的時間是t秒（t＞0）．過點D作DF⊥BC于點F，連接DE、EF．
  （1）求證：AE=DF；
  （2）四邊形AEFD能夠成為菱形嗎？如果能，求出相應的t值；如果不能，說明理由．
  （3）當t為何值時，△DEF為直角三角形？請說明理由．
  組卷：498引用：11難度：0.3

  解析