2019-2020學年北京交大附中九年級（上）開學數學試卷（8月份）

一、選擇題（本題共30分，每小題3分）下面各題均有四個選項，其中只有一個符合題意．

• 1．若代數式

  x

  +

  1

  x

  -

  2

  在實數范圍內有意義，則實數x的取值范圍是（　　）

  A．x≥-1

  B．x＞2

  C．x≠2

  D．x≥-1且x≠2
  組卷：786引用：2難度：0.9

  解析

• 2．在平行四邊形ABCD中，∠A-∠B=50°，則∠D的度數是（　　）

  A．55°

  B．125°

  C．115°

  D．65°
  組卷：26引用：1難度：0.6

  解析

• 3．下列函數的圖象不經過第三象限，且y隨x的增大而減小的是（　　）

  A．y=-3x+1

  B．y=-3x-1

  C．y=3x+1

  D．y=3x-1
  組卷：822引用：4難度：0.8

  解析

• 4．已知2是關于x的方程3x²-2a=0的一個解，則a的值是（　　）

  A．3

  B．4

  C．5

  D．6
  組卷：176引用：5難度：0.9

  解析

• 5．把直線y=-2x向上平移后得到直線AB，若直線AB經過點（m,n），且2m+n=8，則直線AB的表達式為（　　）

  A．y=-2x+4

  B．y=-2x+8

  C．y=-2x-4

  D．y=-2x-8
  組卷：2333引用：15難度：0.7

  解析

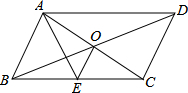• 6．如圖，平行四邊形ABCD的對角線AC，BD交于點O，AE平分∠BAD交BC于點E，且∠ADC=60°，AB=

  1

  2

  BC，連接OE．下列結論：①∠CAD=30°；②S_?ABCD=AB?AC；③OB=AB；④OE=

  1

  4

  BC．其中成立的個數是（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：1670引用：8難度：0.3

  解析

• 7．如圖1是一座立交橋的示意圖（道路寬度忽略不計），A為入口，F，G為出口，其中直行道為AB，CG，EF，且AB=CG=EF；彎道為以點O為圓心的一段弧，且

  ?

  BC

  ，

  ?

  CD

  ，

  ?

  DE

  所對的圓心角均為90°．甲、乙兩車由A口同時駛入立交橋，均以10m/s的速度行駛，從不同出口駛出，其間兩車到點O的距離y（m）與時間x（s）的對應關系如圖2所示．結合題目信息，下列說法錯誤的是（　　）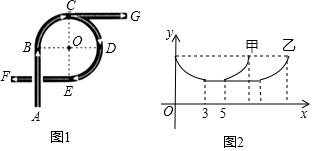
  

  A．甲車在立交橋上共行駛8s

  B．從F口出比從G口出多行駛40m

  C．甲車從F口出，乙車從G口出

  D．立交橋總長為150m
  組卷：665引用：10難度：0.5

  解析

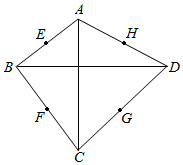• 8．如圖，在四邊形ABCD中，E，F，G，H分別是邊AB，BC，CD，DA中點，AC⊥BD．則下列相關敘述中錯誤的是（　　）

  A．連接EG，FH，則有EG=FH

  B．若BD= 2 AC ，則以E，F，G，H為頂點的四邊形為正方形

  C．連接EG，FH，相交于點O，則OE=OF=OG=OH

  D．若EF=3，FG=4，則EG=5
  組卷：58引用：1難度：0.4

  解析

三、解答題（共46分，第19、21題各5分，20題4分，第22-24題各6分，25-26題各7分）

• 25．在平面直角坐標系xOy中，一次函數y=kx+4（k＜0）交x軸于點A，交y軸于點B．已知△ABO為等腰直角三角形．
  （1）請直接寫出k的值為

  ；
  （2）將一次函數y=kx+4（k≠0）中，直線y=-1下方的部分沿直線y=-1翻折，其余部分保持不變，得到的新圖象記為圖象G．已知在x軸有一動點P（n,0），過點P作x軸的垂線，交

  y

  =

  1

  2

  x

  +

  2

  于點M，交圖象G于點N．當點M在點N上方時，且MN＜2，求n的取值范圍；
  （3）記圖象G交x軸于另一點C，點D為圖象G上一點，點E為圖象G的對稱軸上一點．當以A，C，D，E為頂點的四邊形為平行四邊形時，則點D的坐標為

  ．
  組卷：147引用：1難度：0.2

  解析

• 26．在平行四邊形ABCD中，E是AD上一點，AE=AB，過點E作直線EF，在EF上取一點G，使得∠EGB=∠EAB，連接AG．
  （1）如圖1，當EF與AB相交時，當∠EAB=60°時，
  ①請直接寫出∠C度數為

  ；
  ②求證：EG=AG+BG；
  （2）如圖2，當EF與CD相交時，且∠EAB=90°，請你寫出線段EG，AG，BG之間的數量關系，并證明你的結論．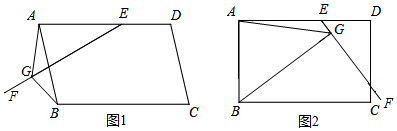
  
  組卷：241引用：2難度：0.2

  解析