2022-2023學年湖北省武漢市水果湖高級中學高一（下）月考數學試卷（3月份）

一、選擇題（共8小題，每小題5，滿分40分）

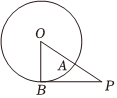• 1．如圖，已知P為圓O外一點（O為圓心），線段PO交圓O于點A，過點P作圓O的切線PB，切點為B，若劣弧AB等分△POB的面積，且∠AOB=α弧度，則（　　）

  A．tanα=α

  B．tanα=2α

  C．sinα=2cosα

  D．2sinα=cosα
  組卷：53引用：2難度：0.8

  解析

• 2．若sin（-140°）=a,則tan40°等于（　　）

  A． a 1 + a 2

  B． - a 1 + a 2

  C． a 1 - a 2

  D． - a 1 - a 2
  組卷：296引用：3難度：0.7

  解析

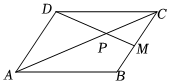• 3．如圖，平行四邊形ABCD中，M為BC中點，AC與MD相交于點P若

  AP

  =x

  AB

  +y

  AD

  ，則x+y=（　　）

  A．1

  B． 4 3

  C． 5 3

  D．2
  組卷：414引用：5難度：0.6

  解析

• 4．函數

  f

  （

  x

  ）

  =

  xcosx

  e

  |

  x

  |

  的圖象大致為（　　）

  A．	B．
  C．	D．
  組卷：258引用：9難度：0.7

  解析

• 5．已知x∈（0，π），則f（x）=cos2x+2sinx的值域為（　　）

  A．（-1， 1 2 ]

  B．（0，2 2 ）

  C．（ 2 2 ， 2 ）

  D．[1， 3 2 ]
  組卷：450引用：11難度：0.7

  解析

• 6．已知

  tan

  （

  α

  +

  π

  6

  ）

  =

  -

  3

  ，則

  sin

  （

  2

  α

  +

  π

  12

  ）

  =（　　）

  A． 2 5 5

  B． - 2 5 5

  C． - 2 10

  D． 2 10
  組卷：230引用：4難度：0.7

  解析

• 7．在四邊形ABCD中，G為△BCD的重心，AG=2，點O在線段AG上，則

  OA

  ?

  （

  OB

  +

  OC

  +

  OD

  ）

  的最小值為（　　）

  A．-3

  B．-2

  C．-1

  D．0
  組卷：97引用：3難度：0.6

  解析

四、解答題（共6小題，滿分70分）

• 21．已知函數f（x）=

  3

  sinωxcosωx-cos²ωx+m.
  （1）若f（x）的圖象關于直線x=

  2

  π

  9

  對稱，ω∈[1，π]，求f（x）的單調遞增區間；
  （2）在（1）的條件下，當x∈[0，

  π

  2

  ]時，x₁和x₂是f（x）的兩個零點，求f（x₁+x₂）-m的值和m的取值范圍．
  組卷：146引用：4難度：0.5

  解析

• 22．已知函數f（x）=-9（|sinx|+|cosx|）+4sin2x+9．
  （1）求出f（x）的最小正周期，并證明；（“周期”要證，“最小”不用證明）
  （2）若x∈[0，

  π

  2

  ]，求f（x）的值域；
  （3）是否存在正整數n,使得f（x）=0在區間[0，nπ]內恰有2001個根，若存在，求出n的值：若不存在，說明理由．
  組卷：90引用：2難度：0.4

  解析