2022-2023學年江西省南昌二十八中教育集團江鈴學校九年級（上）開學數(shù)學試卷

一、選擇題（本大題共6小題，共18分。在每小題列出的選項中，選出符合題目的一項）

• 1．若

  a

  -

  1

  有意義，則a的取值范圍是（　　）

  A．a(chǎn)≥1

  B．a(chǎn)≤1

  C．a(chǎn)≥0

  D．a(chǎn)≤-1
  組卷：1243引用：21難度：0.9

  解析

• 2．下列各式是最簡二次根式的是（　　）

  A． 13

  B． 12

  C． a 3 （ a ≥ 0 ）

  D． 5 3
  組卷：110引用：3難度：0.7

  解析

• 3．已知直角三角形的兩邊長分別為3和5，則第三邊長是（　　）

  A．4

  B． 34

  C．4或 34

  D．7
  組卷：708引用：8難度：0.5

  解析

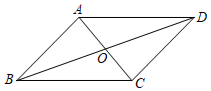• 4．如圖，?ABCD的對角線AC，BD相交于點O，則下列結論一定正確的是（　　）

  A．OB=OD

  B．AB=BC

  C．AC⊥BD

  D．∠ABD=∠CBD
  組卷：1297引用：21難度：0.6

  解析

• 5．如圖，在平面直角坐標系中，一次函數(shù)y=x+1的圖象是（　　）

  A．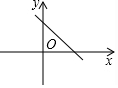

  B．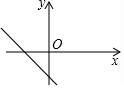

  C．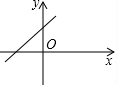

  D．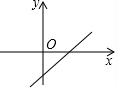
  組卷：197引用：16難度：0.9

  解析

• 6．一次數(shù)學測驗中，某學習小組六名同學的成績（單位：分）分別是110，90，105，91，85，95．則該小組的平均成績是（　　）

  A．94分

  B．95分

  C．96分

  D．98分
  組卷：373引用：10難度：0.9

  解析

二、填空題（本大題共6小題，共18分）

• 7．化簡

  12

  的結果為

  ．
  組卷：742引用：26難度：0.7

  解析

三、解答題（本大題共11小題。解答應寫出文字說明，證明過程或演算步驟）

• 22．數(shù)學概念
  我們把對角線相等的四邊形稱為等對角線四邊形．
  回憶舊知
  （1）在我們學習過的四邊形中，找出一個等對角線四邊形，寫出它的名稱．
  知識運用
  （2）已知四邊形ABCD是等對角線四邊形，圖①中四邊形EFGH的四個頂點分別是四邊形ABCD四條邊的中點，圖②中四邊形KLMN的邊KL∥MN∥AC，邊ML∥NK∥BD，則

   

  
  A．四邊形EFGH、KLMN都是等對角線四邊形
  B．四邊形EFGH、KLMN都不是等對角線四邊形
  C．四邊形EFGH是等對角線四邊形，四邊形KLMN不是等對角線四邊形
  D．四邊形EFGH不是等對角線四邊形，四邊形KLMN是等對角線四邊形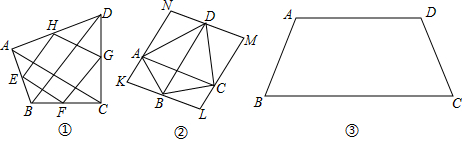
  
  概念證明
  （3）規(guī)定：一組對邊平行且不相等，另一組對邊相等的四邊形為“等腰梯形”，請嘗試證明等腰梯形是等對角線四邊形．
  已知：如圖③，在等腰梯形ABCD中，AD∥BC，AD≠BC，AB=CD．
  求證：等腰梯形ABCD是等對角線四邊形．
  類比遷移
  在七年級（下）學習三角形的時候，我們曾用來揭示三角形和一些特殊三角形之間的關系：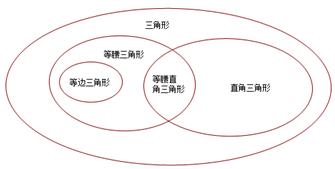
  
  （4）請用類似的方法揭示四邊形、等對角線四邊形、平行四邊形、矩形、正方形、等腰梯形之間的關系．
  組卷：305引用：2難度：0.1

  解析

• 23．（1）模型建立：如圖1，等腰直角三角形ABC中，∠ACB=90°，CB=CA，直線ED經(jīng)過點C，過A作AD⊥ED于D，過B作BE⊥ED于E．求證：△BEC≌△CDA；
  （2）模型應用：已知直線y=2x+4與y軸交于A點，與x軸交于B點，在AB左側過點B作線段BC，使BC=AB，BC⊥AB，過點A，C作直線，求直線AC的解析式；
  （3）如圖3，矩形ABCO，O為坐標原點，B的坐標為（6，4），A，C分別在坐標軸上，P是線段BC上動點，已知點D在第一象限，且是直線y=2x-5上的一點，若△APD是不以A為直角頂點的等腰直角三角形，請直接寫出所有符合條件的點D的坐標．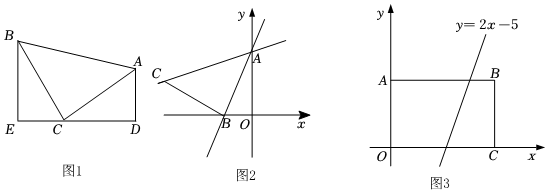
  
  組卷：501引用：2難度：0.3

  解析