當(dāng)前位置：試卷中心 > 試卷詳情

2022-2023學(xué)年山西省太原師范學(xué)院附中八年級（上）第一次月考數(shù)學(xué)試卷

發(fā)布：2024/4/20 14:35:0

一、選擇題：（本大題共10個小題，每小題3分，共30分，在每個小題給出的四個選項中，只有一項符合題目要求，請選出并將答案填在答題紙的表格內(nèi)）

1．下列是無理數(shù)的是（　　）
A．3.1415926 B．
9
4
C．
22
7
D．
5
組卷：25引用：1難度：0.7
解析
2．下列二次根式中，是最簡二次根式的是（　　）
A．
27
B．
18
C．
15
D．
3
2
組卷：95引用：2難度：0.8
解析
3．我國是最早了解勾股定理的國家之一，早在三千多年前，周朝數(shù)學(xué)家商高就提出了“勾三、股四、弦五”這一結(jié)論，被記載于我國古代一部著名的數(shù)學(xué)著作中，這部著作是（　　）
A．
《孫子算經(jīng)》 B．
《海島算經(jīng)》 C．
《九章算術(shù)》 D．
《周髀算經(jīng)》
組卷：218引用：8難度：0.9
解析
4．若直角三角形三邊的長分別是正整數(shù)a,b,c,則下列各組數(shù)一定還是直角三角形三邊長的是（　　）
A．
1
3
a
，
1
3
b
，
1
3
c
B．a(chǎn)+1，b+1，c+1
C．a(chǎn)²，b²，c² D．a(chǎn)-2，b-2，c-2
組卷：113引用：1難度：0.7
解析
5．下列計算正確的是（　　）
A．
25
=±
5
B．
24
4
=
6
C．
10
+
8
=
18
D．
18
+
2
=
4
2
組卷：141引用：2難度：0.8
解析
6．如圖，用邊長為3的兩個小正方形拼成一個大正方形，則大正方形的邊長最接近的整數(shù)是（　　）
A．3 B．4 C．5 D．6
組卷：3025引用：29難度：0.7
解析
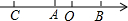7．如圖，數(shù)軸上A，B兩點表示的數(shù)分別為-1和
3
，點B關(guān)于點A的對稱點為C，則點C所表示的數(shù)為（　　）
A．-2-
3
B．-1-
3
C．-2+
3
D．1+
3
組卷：2021引用：113難度：0.7
解析

當(dāng)前模式為游客模式，立即登錄查看試卷全部內(nèi)容及下載

三、解答題：（本大題共6個小題，共49分，要有必要文字說明、證明過程或演算步驟）

22．閱讀材料：
小明在學(xué)習(xí)二次根式后，發(fā)現(xiàn)一些含根號的式子可以寫成另一個式子的平方，如3+
2
2
=（1+
2
）²．善于思考的小明進(jìn)行了以下探索：
設(shè)a+b
2
=（m+n
2
）²（其中a、b、m、n均為整數(shù)），則有a+b
2
=m²+2n²+2mn
2
．
∴a=m²+2n²，b=2mn.這樣小明就找到了一種把類似a+b
2
的式子化為平方式的方法．
請你仿照小明的方法探索并解決下列問題：
（1）當(dāng)a、b、m、n均為正整數(shù)時，若a+b
3
=
（
m
+
n
3
）
2
，用含m、n的式子分別表示a、b,得：a=
，b=
；
（2）利用所探索的結(jié)論，找一組正整數(shù)a、b、m、n填空：
+
3
=（
+
3
）²；
（3）若a+4
3
=
（
m
+
n
3
）
2
，且a、m、n均為正整數(shù)，求a的值？
組卷：7780引用：111難度：0.5
解析
23．定義：如圖①，點M、N把線段AB分割成AM、MN和BN，若以AM、MN、BN為邊的三角形是一個直角三角形，則稱點M、N是線段AB的勾股分割點．

（1）已知點M、N是線段AB的勾股分割點，若AM=2，MN=3，則BN²=
；
（2）如圖②，在等腰直角△ABC中，AC=BC，∠ACB=90°，點M、N為邊AB上兩點，滿足∠MCN=45°，求證：點M、N是線段AB的勾股分割點．
陽陽同學(xué)在解決第（2）小題時遇到了困難，陳老師對陽陽說：要證明勾股分割點，則需設(shè)法構(gòu)造直角三角形．
請你根據(jù)陽陽同學(xué)的思路將第（2）小題的證明過程補(bǔ)寫完整；
證明：把△CBN繞點C逆時針旋轉(zhuǎn)90°，得到△CAN'，連接MN'
∴△AN'C≌△BNC
∴CN'=CN，∠ACN'=∠BCN，∠CBN=∠CAN'
∵∠MCN=45°，∠ACB=90°
∴∠N'CA+∠ACM=∠ACM+∠BCN=∠ACB-∠MCN=45°
∴……
（3）在（2）的問題中，若∠ACM=15°，AM=1，CM=
3
+1，請直接寫出BM的長．（提示：在直角三角形中，30°角所對的直角邊等于斜邊的一半）
組卷：224引用：2難度：0.2
解析