2022-2023學(xué)年吉林省第二實驗遠洋學(xué)校八年級（上）第一次達標(biāo)檢測數(shù)學(xué)試卷

一.選擇題

• 1．如圖所示，△ABC≌△ADE，∠B=30°，∠C=95°，∠EAD的度數(shù)是（　　）

  A．44°

  B．55°

  C．66°

  D．77°
  組卷：1129引用：16難度：0.7

  解析

• 2．用反證法證明命題“若|a|＜3，則a²＜9”時，應(yīng)假設(shè)（　　）

  A．a(chǎn)＞3

  B．a(chǎn)≥3

  C．a(chǎn)2≥9

  D．a(chǎn)2＞9
  組卷：702引用：10難度：0.7

  解析

• 3．下列命題正確的是（　　）

  A．被開方數(shù)越大，對應(yīng)的立方根也越大

  B．直線外一點到這條直線的垂線段，叫做點到直線的距離

  C．內(nèi)錯角相等

  D．無限小數(shù)都是無理數(shù)
  組卷：129引用：4難度：0.8

  解析

• 4．如圖，∠1=∠2，添加下列條件，不能使△ABC≌△BAD的是（　　）

  A．∠CAB=∠DBA

  B．AC=BD

  C．∠C=∠D

  D．AD=BC
  組卷：1032引用：7難度：0.7

  解析

• 5．如圖，用尺規(guī)作圖作出∠OBF=∠AOB，則作圖痕跡弧MN是（　　）

  A．以點B為圓心，以O(shè)D長為半徑的弧

  B．以點B為圓心，以DC長為半徑的弧

  C．以點E為圓心，以O(shè)D長為半徑的弧

  D．以點E為圓心，以DC長為半徑的弧
  組卷：678引用：8難度：0.7

  解析

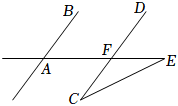• 6．某城市幾條道路的位置關(guān)系如圖所示，道路AB∥CD，道路AB與AE的夾角∠BAE=50°．城市規(guī)劃部門想新修一條道路CE，要求CF=EF，則∠E的度數(shù)為（　　）

  A．23°

  B．25°

  C．27°

  D．30°
  組卷：1325引用：9難度：0.7

  解析

• 7．如圖，在四個均由十六個小正方形組成的正方形網(wǎng)格中，各有一個三角形，那么這四個三角形中，不是直角三角形的是（　　）

  A．

  B．

  C．

  D．
  組卷：413引用：4難度：0.6

  解析

三、解答題

• 21．如圖，長方形ABCD中，AB=4cm,BC=6cm,現(xiàn)有一動點P從A出發(fā)以2cm/秒的速度，沿矩形的邊A-B-C-D-A返回到點A停止，設(shè)點P運動的時間為t秒．
  （1）當(dāng)t=3時，BP=

  cm；
  （2）當(dāng)t為何值時，連接CP，DP，△CDP是等腰三角形；
  （3）Q為AD邊上的點，且DQ=5，當(dāng)t為何值時，以長方形的兩個頂點及點P為頂點的三角形與△DCQ全等．
  
  組卷：1459引用：7難度：0.5

  解析

• 22．通過對如圖數(shù)學(xué)模型的研究學(xué)習(xí)，解決下列問題：
  （1）如圖1，∠BAD=90°，AB=AD，過點B作BC⊥AC于點C，過點D作DE⊥AC于點E．由∠1+∠2=∠2+∠D=90°，得∠1=∠D．又∠ACB=∠AED=90°，可以推理得到△ABC≌△DAE．進而得到AC=

  ，BC=AE．我們把這個數(shù)學(xué)模型稱為“K字”模型或“一線三等角”模型；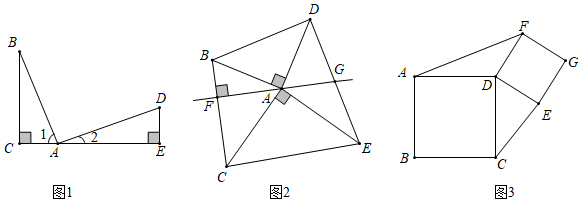
  
  （2）如圖2，∠BAD=∠CAE=90°，AB=AD，AC=AE，連接BC，DE，且BC⊥AF于點F，DE與直線AF交于點G．求證：點G是DE的中點；
  （深入探究）
  （3）如圖，已知四邊形ABCD和DEGF為正方形，△AFD的面積為S₁，△DCE的面積為S₂，S₁+S₂=10，直接寫出S₁的值．
  組卷：853引用：3難度：0.1

  解析