2022-2023學年上海市普陀區高三（上）期末數學試卷（一模）

一、填空題（本大題共有12題，滿分54分，第1-6題每題4分，第7-12題每題5分）考生應在答題紙的相應位置直接填寫結果．

• 1．若z=i?（1-i）（其中i表示虛數單位），則Imz=

  ．
  組卷：73引用：1難度：0.8

  解析

• 2．若正四棱柱的底面周長為4、高為2，則該正四棱柱的體積為

  ．
  組卷：88引用：2難度：0.6

  解析

• 3．設

  y

  =

  x

  1

  2

  -

  x

  3

  ，則滿足y＜0的x的取值范圍為

  ．
  組卷：109引用：5難度：0.7

  解析

• 4．函數y=tan2x在區間

  （

  -

  π

  4

  ，

  π

  4

  ）

  上的零點為

  ．
  組卷：83引用：1難度：0.7

  解析

• 5．函數y=1-2sin²x的最小正周期為

  ．
  組卷：117引用：2難度：0.7

  解析

• 6．在（x+1）⁴+（x+1）⁵展開式中，含有x²項的系數為

  ．
  組卷：145引用：1難度：0.8

  解析

• 7．雙曲線

  x

  2

  3

  -

  y

  2

  =

  1

  的兩條漸近線的夾角大小等于

  ．
  組卷：198引用：9難度：0.7

  解析

三、解答題（本大題共有5題，滿分78分），解答下列各題必須在答題紙的相應位置寫出必要的步驟．

• 20．在xoy坐標平面內，已知橢圓Γ：

  x

  2

  9

  +

  y

  2

  5

  =1的左、右焦點分別為F₁、F₂，直線y=k₁x（k₁≠0）與Γ相交于A、B兩點．
  （1）記d為A到直線2x+9=0的距離，當k₁變化時，求證：

  |

  A

  F

  1

  |

  d

  為定值；
  （2）當∠AF₂B=120°時，求|AF₂|?|BF₂|的值；
  （3）過B作BM⊥x軸，垂足為M，OM的中點為N，延長AN交Γ于另一點P，記直線PB的斜率為k₂，當k₁取何值時，|k₁-k₂|有最小值？并求出此最小值．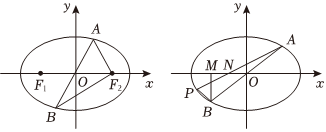
  
  組卷：245引用：3難度：0.2

  解析

• 21．若函數y=f（x）（x∈D）同時滿足下列兩個條件，則稱y=f（x）在D上具有性質M．
  ①y=f（x）在D上的導數f′（x）存在；
  ②y=f′（x）在D上的導數f″（x）存在，且f″（x）＞0（其中f″（x）=[f′（x）]′）恒成立．
  （1）判斷函數y=lg

  1

  x

  在區間（0，+∞）上是否具有性質M？并說明理由．
  （2）設a、b均為實常數，若奇函數g（x）=2x³+ax²+

  b

  x

  在x=1處取得極值，是否存在實數c,使得y=g（x）在區間[c,+∞）上具有性質M？若存在，求出c的取值范圍；若不存在，請說明理由．
  （3）設k∈Z且k＞0，對于任意的x∈（0，+∞），不等式

  1

  +

  ln

  （

  x

  +

  1

  ）

  x

  ＞

  k

  x

  +

  1

  成立，求k的最大值．
  組卷：237引用：4難度：0.4

  解析