2016-2017學年山東省淄博市桓臺二中高三（下）開學數學試卷（理科）

一、選擇題：本大題共10小題，每小題5分，共50分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知不等式|x-2|＜3的解集為A，函數y=ln（1-x）的定義域為B，則圖中陰影部分表示的集合為（　　）

  A．{x∈R|-1＜x＜1}

  B．{x∈R|1≤x＜5}

  C．{x∈R|1＜x＜5}

  D．{x∈R|x≥1}
  組卷：44引用：1難度：0.9

  解析

• 2．已知a∈R，i是虛數單位，命題p：在復平面內，復數z₁=a+

  2

  1

  -

  i

  對應的點位于第二象限；命題q：復數z₂=a-i的模等于2，若p∧q是真命題，則實數a的值等于（　　）

  A．-1或1

  B． - 3 或 3

  C． - 5

  D． - 3
  組卷：70引用：7難度：0.7

  解析

• 3．已知定義在R上的函數f（x）=2^|x|，記a=f（log_0.53），b=f（log₂5），c=f（0），則a,b,c的大小關系為（　　）

  A．a＜b＜c

  B．c＜a＜b

  C．a＜c＜b

  D．c＜b＜a
  組卷：533引用：6難度：0.9

  解析

• 4．已知θ為銳角，且cos（θ+

  π

  12

  ）=

  3

  3

  ，則cos（

  5

  π

  12

  -θ）=（　　）

  A． 6 + 2 4

  B． 1 2

  C． 6 3

  D．- 6 3
  組卷：89引用：4難度：0.9

  解析

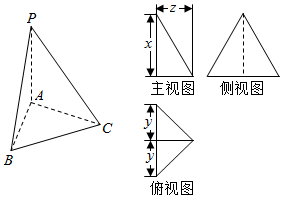• 5．如圖，已知三棱錐P-ABC的底面是等腰直角三角形，且∠ACB=

  π

  2

  ，側面PAB⊥底面ABC，AB=PA=PB=2．則這個三棱錐的三視圖中標注的尺寸x,y,z分別是（　　）

  A． 3 ，1， 2

  B． 3 ，1，1

  C．2，1， 2

  D．2，1，1
  組卷：124引用：5難度：0.7

  解析

• 6．已知某工程在很大程度上受當地年降水量的影響，施工期間的年降水量X（單位：mm）對工期延誤天數Y的影響及相應的概率P如表所示：

  降水量X	X＜100	100≤X＜200	200≤X＜300	X≥300
  工期延誤天數Y	0	5	15	30
  概率P	0.4	0.2	0.1	0.3

  在降水量X至少是100的條件下，工期延誤不超過15天的概率為（　　）

  A．0.1

  B．0.3

  C．0.42

  D．0.5
  組卷：120引用：4難度：0.7

  解析

• 7．設實數x,y滿足約束條件

  x ≥ 1

  y ≥ 1

  x + y - 4 ≤ 0

  ，若對于任意b∈[0，1]，不等式ax-by＞b恒成立，則實數a的取值范圍是（　　）

  A．（ 2 3 ，4）

  B．（ 2 3 ，+∞）

  C．（2，+∞）

  D．（4，+∞）
  組卷：18引用：2難度：0.7

  解析

三、解答題：本大題共6小題，共75分．

• 20．已知二次函數f（x）=

  1

  3

  x²+

  2

  3

  x.數列{a_n}的前n項和為S_n，點（n,S_n）（n∈N^*）在二次函數y=f（x）的圖象上．
  （Ⅰ）求數列{a_n}的通項公式；
  （Ⅱ）設b_n=a_na_n+1cos[（n+1）π]（n∈N^*），數列{b_n}的前n項和為T_n，若T_n≥tn²對n∈N^*恒成立，求實數t的取值范圍；
  （Ⅲ）在數列{a_n}中是否存在這樣一些項：

  a

  n

  1

  ，

  a

  n

  2

  ，

  a

  n

  3

  ，…，

  a

  n

  k

  這些項都能夠
  構成以a₁為首項，q（0＜q＜5）為公比的等比數列{

  a

  n

  k

  }？若存在，寫出n_k關于f（x）的表達式；若不存在，說明理由．
  組卷：81引用：2難度：0.1

  解析

• 21．已知函數f（x）=

  ex

  e

  x

  ．
  （Ⅰ）求函數f（x）極值；
  （Ⅱ）若直線y=ax+b是函數f（x）的切線，求a-b的最大值；
  （Ⅲ）若方程f（x）=m存在兩個實數根x₁，x₂，且x₁+x₂=2x₀．
  ①求證：0＜m＜1；
  ②問：函數f（x）圖象上在點（x₀，f（x₀））處的切線是否能平行x軸？若存在，求出該切線；若不存在說明理由．
  組卷：45引用：1難度：0.1

  解析