2021-2022學年江蘇省鹽城市響水二中高二（下）期中數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知空間向量

  a

  =（-3，2，5），

  b

  =（1，x,-1），且

  a

  與

  b

  垂直，則x等于（　　）

  A．4

  B．1

  C．3

  D．2
  組卷：141引用：11難度：0.8

  解析

• 2．已知

  C

  x

  +

  2

  18

  =

  C

  2

  x

  -

  5

  18

  ，則x的取值為（　　）

  A．7

  B．8

  C．9

  D．10
  組卷：191引用：4難度：0.8

  解析

• 3．已知

  a

  =

  （

  1

  ，

  0

  ，

  0

  ）

  ，

  b

  =

  （

  x

  ,

  1

  ，

  2

  ）

  ，向量

  a

  與

  b

  的夾角

  π

  4

  ，則x=（　　）

  A． ± 5

  B． 5

  C． - 5

  D．0
  組卷：2引用：1難度：0.8

  解析

• 4．已知隨機變量X的分布列為（　　）
  

  X	0	1	2
  P	1 3	1 3	1 3

  設Y=2X+3，則D（Y）等于（　　）

  A． 5 3

  B． 8 3

  C． 2 3

  D． 1 3
  組卷：222引用：5難度：0.9

  解析

• 5．口袋中裝有大小形狀相同的紅球3個，白球3個，小明從中不放回的逐一取球，已知在第一次取得紅球的條件下，第二次取得白球的概率為（　　）

  A．0.4

  B．0.5

  C．0.6

  D．0.75
  組卷：950引用：8難度：0.8

  解析

• 6．從5臺原裝計算機和4臺組裝計算機中任意選取5臺，其中至少有原裝與組裝計算機各2臺，則不同的選取方法有（　　）

  A．300種

  B．200種

  C．150種

  D．100種
  組卷：121引用：4難度：0.8

  解析

• 7．已知（3x-1）（x+1）ⁿ的展開式中所有項的系數之和為64，則展開式中含有x³的項系數為（　　）

  A．20

  B．30

  C．45

  D．60
  組卷：239引用：3難度：0.7

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．某地舉行象棋比賽，淘汰賽階段的比賽規(guī)則是：兩人一組，先勝一局者進入復賽，敗者淘汰．比賽雙方首先進行一局慢棋比賽，若和棋，則加賽快棋；若連續(xù)兩局快棋都是和棋，則再加賽一局超快棋，超快棋只有勝與負兩種結果．在甲與乙的比賽中，甲慢棋比賽勝與和的概率分別為

  1

  2

  ，

  1

  3

  ，快棋比賽勝與和的概率均為

  1

  3

  ，超快棋比賽勝的概率為

  1

  4

  ，且各局比賽相互獨立．
  （1）求甲恰好經過三局進入復賽的概率；
  （2）記淘汰賽階段甲與乙比賽的局數為X，求X的概率分布列和數學期望．
  組卷：454引用：5難度：0.4

  解析

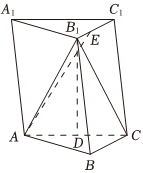• 22．如圖，在三棱柱ABC-A₁B₁C₁中，B₁A=B₁C，AA₁=13，AB=8，BC=6，AB⊥BC，D為AC中點，

  tan

  ∠

  B

  B

  1

  D

  =

  5

  12

  ．
  （1）求證：BC⊥B₁D；
  （2）線段B₁C₁上是否存在一點E，使得AE與面BCC₁B₁的夾角的正弦值為

  12

  74

  185

  ？若存在，求出E點的位置；若不存在，請說明理由．
  組卷：10引用：1難度：0.5

  解析