當前位置：試卷中心 > 試卷詳情

2022-2023學年江蘇省常州外國語學校八年級（上）期中數學試卷

發布：2024/7/26 8:0:9

一、選擇題（每題3分，共24分）

1．第24屆冬奧會將于2022年在北京和張家口舉辦．下列四個圖分別是第24屆冬奧會圖標中的一部分，其中是軸對稱圖形的是（　　）
A． B． C． D．
組卷：325引用：8難度：0.9
解析
2．下列各數中，是無理數的是（　　）
A．
1
7
B．
2
C．0.5 D．
9
組卷：73引用：2難度：0.9
解析
3．下列計算正確的是（　　）
A．
3
2
+
2
=
4
2
B．
5
2
-
3
2
=
5
-
3
C．
18
÷
3
=
6
D．
8
-
3
=
5
組卷：114引用：2難度：0.8
解析
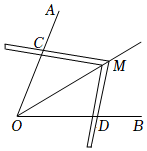4．工人師傅常常利用角尺構造全等三角形的方法來平分一個角．如圖，在∠AOB的兩邊OA、OB上分別在取OC=OD，移動角尺，使角尺兩邊相同的刻度分別與點C、D重合，這時過角尺頂點M的射線OM就是∠AOB的平分線，這里構造全等三角形的依據是（　　）
A．SSS B．ASA C．AAS D．SAS
組卷：3218引用：34難度：0.7
解析
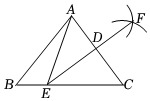5．如圖，在△ABC中，點D是AC的中點，分別以點A，C為圓心，大于
1
2
AC的長為半徑作弧，兩弧交于F，直線FD交BC于點E，連接AE，若AD=2，△ABE的周長為12，則△ABC的周長為（　　）
A．13 B．14 C．15 D．16
組卷：1841引用：15難度：0.6
解析
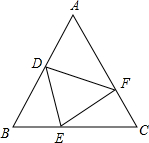6．如圖，△ABC中，AB=AC，BD=CE，BE=CF，若∠A=40°，則∠DEF的度數是（　　）
A．75° B．70° C．65° D．60°
組卷：2577引用：6難度：0.9
解析
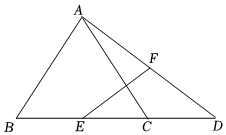7．如圖，△ABC中，AB=AC，點D在BC的延長線上，連接AD，點E、F分別是BC、AD的中點，若EF=3，則AD的長為（　　）
A．3 B．3
3
C．3
2
D．6
組卷：218引用：1難度：0.5
解析
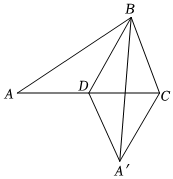8．如圖，在△ABC中、D是邊AC中點，連接BD，將△ABD沿線段BD翻折后得△A′BD，其中A′C=4，AD=4，AB=
37
，則D到AB邊的距離為（　　）
A．
8
111
37
B．
6
111
37
C．
5
111
37
D．
10
111
37
組卷：178引用：1難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（19題20題各8分，21題6分，22題8分，23題6分，24題11分，25題9分）

24．如圖1，在△ABC中，AB=AC，D為射線BC上（不與B、C重合）一動點，在AD的右側射線BC的上方作△ADE，使得AD=AE，∠DAE=∠BAC，連接CE．

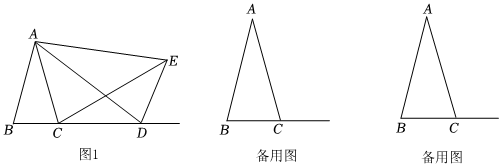
（1）找出圖中的一對全等三角形，并證明你的結論；
（2）延長EC交AB的延長線于點F，若∠F=45°，
①利用（1）中的結論求出∠DCE的度數；
②當△ABD是等腰三角形時，直接寫出∠ADB的度數；
（3）當D在線段BC上時，若線段BC=3，△ABC面積為3，則四邊形ADCE周長的最小值是
．
組卷：570引用：2難度：0.2
解析
25．數與形是數學中的兩個最古老，也是最基本的研究對象，它們在一定條件下可以相互轉化，數形結合就是把抽象的數學語言、數量關系與直觀的幾何圖形、位置關系結合起來，通過“以形助數”或“以數解形”可以使復雜問題簡單化，抽象問題具體化，從而起到優化解題途徑的目的．
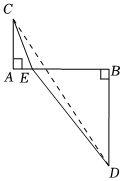
（1）【思想應用】已知m,n均為正實數、且m+n=2，求
m
2
+
1
+
n
2
+
4
的最小值．通過分析，小明想到了利用下面的構造解決此問題：如圖，AB=2，AC=1，BD=2，AC⊥AB，BD⊥AB，點E是線段AB上的動點，且不與端點重合，連接CE，DE，設AE=m,BE=n.
①用含m的代數式表示CE=
，用含n的代數式表示DE=
；
②據此寫出
m
2
+
1
+
n
2
+
4
的最小值
；
（2）【類比應用】根據上述的方法，代數式
x
2
+
25
+
（
x
-
16
）
2
+
49
的最小值是
；
（3）【拓展應用】
①已知a,b,c為正數，且a+b+c=1，試運用構圖法，畫出圖形，并寫出
a
2
+
b
2
+
b
2
+
c
2
+
c
2
+
a
2
的最小值；
②若a,b為正數，寫出以
a
2
+
b
2
，
4
a
2
+
b
2
，
a
2
+
4
b
2
為邊的三角形的面積
．
組卷：567引用：2難度：0.2
解析