2023-2024學年吉林省長春市第二中學高二（上）第一次學程數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知A（0，2），B（2，1），過點C（1，0）且斜率為k的直線l與線段AB有公共點，則k的取值范圍是（　　）

  A．[-2，1]	B．（-∞，-2）∪（1，+∞）
  C．（-2，1）	D．（-∞，-2]∪[1，+∞）
  組卷：877引用：6難度：0.6

  解析

• 2．已知直線l₁：mx+2y-2=0與直線l₂：5x+（m+3）y-5=0，若l₁∥l₂，則m=（　　）

  A．-5

  B．2

  C．2或-5

  D．5
  組卷：371引用：24難度：0.7

  解析

• 3．M（x,y）為圓C：x²+y²-4x-2y+1=0上任意一點，且點Q（-1，-3）．則|MQ|的最大值為（　　）

  A．5

  B．9

  C．8

  D．7
  組卷：74引用：2難度：0.7

  解析

• 4．直線l：y=kx+1與圓O：x²+y²=1相交于A，B兩點，則“k=1”是“

  |

  AB

  |

  =

  2

  ”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：114引用：11難度：0.9

  解析

• 5．我國古代數學名著《九章算術》對立體幾何問題有著深入的研究，從其中的一些數學用語可見．譬如“塹堵”指底面為直角三角形且側棱垂直于底面的三棱柱，“陽馬”指底面是矩形且有一側棱垂直于底面的四棱錐，“鱉臑”指四個面都是直角三角形的三棱錐．現有一如圖所示的“塹堵”ABC-A₁B₁C₁，其中AC⊥BC，若AA₁=AC=BC=4，則A到平面A₁BC₁的距離為（　　）

  A． 2

  B． 2 2

  C． 2 2

  D． 2 3
  組卷：53引用：1難度：0.6

  解析

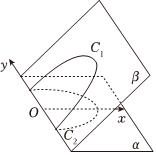• 6．如圖二面角α-y-β的大小為60°，平面β上的曲線C₁是橢圓的一部分，平面α上的曲線C₂是圓的一部分，平面β上的曲線C₁在平面α上的正投影為曲線C₂，曲線C₂在直角坐標系xOy下的方程x²+y²=4（0≤x≤2），則曲線C₁的離心率為（　　）

  A． e = 1 3

  B． e = 5 3

  C． e = 3 2

  D． e = 1 2
  組卷：28引用：1難度：0.7

  解析

• 7．已知點P是直線l₁：mx-ny-5m+n=0和l₂：nx+my-5m-n=0（m,n∈R，m²+n²≠0）的交點，點Q是圓C：（x+1）²+y²=1上的動點，則|PQ|的最大值是（　　）

  A． 5 + 2 2

  B． 6 + 2 2

  C． 5 + 2 3

  D． 6 + 2 3
  組卷：243引用：11難度：0.6

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

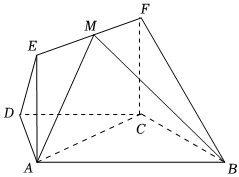• 21．在梯形ABCD中，AB∥CD，AD=DC=CB=1，∠ABC=60°，四邊形ACFE為矩形，平面ACFE⊥平面ABCD，CF=1．
  （1）求證：BC⊥平面ACFE；
  （2）若點M在線段EF上運動，設平面MAB與平面FCB的夾角為θ，試求cosθ的范圍．
  組卷：204引用：3難度：0.3

  解析

• 22．設圓O₁：

  （

  x

  -

  2

  ）

  2

  +

  y

  2

  =

  16

  的圓心為O₁，點O₂與點O₁關于原點對稱，P是圓O₁上任意一點，線段PO₂的垂直平分線交線段PO₁于點M，記點M的軌跡為曲線C．
  （1）求曲線C的方程；
  （2）已知點A（-2，0），曲線C上是否存在點B，使得在y軸上能找到一點D滿足△ABD為等邊三角形？若存在，求出所有點B的坐標；若不存在，請說明理由．
  組卷：59引用：2難度：0.6

  解析