2023-2024學年上海市楊浦高級中學高一（上）期中數學試卷

一、填空題（3'×10=30'）

• 1．若指數函數的圖像經過點

  （

  2

  ，

  1

  4

  ）

  ，則指數函數的解析式為

  ．
  組卷：660引用：5難度：0.8

  解析

• 2．滿足{1，2}?A?{1，2，3，4，5}的集合A有

  個．
  組卷：515引用：13難度：0.7

  解析

• 3．關于x的不等式ax²+bx+2＞0的解集為{x|-2＜x＜3}，則b的值為

  ．
  組卷：179引用：4難度：0.8

  解析

• 4．已知a,b為正數，化簡

  a

  5

  b

  2

  ?

  （

  a

  2

  b

  ）

  -

  1

  ?

  b

  3

  =

  ．
  組卷：268引用：4難度：0.7

  解析

• 5．已知log₁₈9=a,18^b=5，則log₃₆45=

  （用a,b表示）．
  組卷：3164引用：11難度：0.7

  解析

• 6．不等式x²-3＞2|x|的解集是

   

  ．
  組卷：41引用：2難度：0.7

  解析

三、簡答題

• 18．設函數

  y

  =

  1

  |

  x

  |

  -

  1

  ．
  （1）在如圖平面直角坐標系中畫出函數的圖像；
  （2）試說明函數圖象關于y軸對稱；
  （3）解不等式

  1

  |

  x

  |

  -

  1

  ＞

  x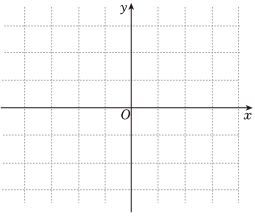

  ．
  
  組卷：31引用：1難度：0.5

  解析

• 19．某科研小組對面積為8000平方米的某池塘里的一種生物的生長規律進行研究，一開始在此池塘投放了一定面積的該生物，觀察實驗得到該生物覆蓋面積y（單位：平方米）與所經過月數x（x∈N）的下列數據：
  

  x	0	2	3	4
  y	4	25	62.5	156.25

  為描述該生物覆蓋面積y（單位：平方米）與經過的月數x（x∈N）的關系，現有以下三種函數模型供選擇：y=k?a^x（k＞0，a＞1）；y=p

  x

  +q（p＞0）；y=ax²+bx+c.
  （1）試判斷哪個函數模型更適合，并求出該模型的函數解析式；
  （2）約經過幾個月，此生物能覆蓋整個池塘？
  （3）經過4個月的研究掌握該生物生長規律后，科研小組需改善池塘生態，現有兩種方案：
  方案一：加入能抑制該生物生長的某種化學物質，使其覆蓋面積y與經過的月數x（x≥5）的關系變為y=4?1.7^x；
  方案二：在4月底集中打撈一次，使其覆蓋面積減少到4平方米，生物增長速度不變．
  問如何評價這兩種方案，并說明理由．
  組卷：38引用：1難度：0.5

  解析