2022-2023學年陜西省渭南市臨渭區九年級(上)期末數學試卷
發布:2024/11/10 0:0:2
一.選擇題(共8小題,每小題3分,計24分,每小題只有一個選項是符合題意的).
-
 1.如圖所示的幾何體,其主視圖是( )
1.如圖所示的幾何體,其主視圖是( )A. 
B. 
C. 
D.  組卷:724引用:5難度:0.7
組卷:724引用:5難度:0.7 -
 2.如圖,兩條直線被三條平行線所截,已知AB=3,DE=4,EF=8,則AC的長是( )
2.如圖,兩條直線被三條平行線所截,已知AB=3,DE=4,EF=8,則AC的長是( )A.9 B. 413C. 92D.7 組卷:265引用:3難度:0.8 -
3.已知反比例函數y=
(k≠0)與正比例函數y=-2x沒有交點,且雙曲線圖象上有三點A(-1,a)、B(-3,b)、C(4,c),則a、b、c的大小關系為( )kxA.a>b>c B.b>a>c C.c>b>a D.c>a>b 組卷:846引用:4難度:0.6 -
4.設a,b是方程x2+x-2020=0的兩個實數根,則(a-1)(b-1)的值為( )
A.-2022 B.2018 C.-2018 D.2022 組卷:279引用:1難度:0.6 -
5.一個不透明的箱子里裝有m個球,其中紅球3個,這些球除顏色不同其余都相同,每次攪拌均勻后,任意摸出一個球記下顏色后再放回,大量重復試驗發現,摸到紅球的頻率穩定在0.3附近,則可以估算出m的值為( )
A.3 B.5 C.10 D.12 組卷:671引用:15難度:0.8 -
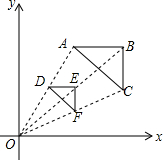 6.如圖,△ABC中,A(2,4)以原點為位似中心,將△ABC縮小后得到△DEF,若D(1,2),△DEF的面積為4,則△ABC的面積為( )
6.如圖,△ABC中,A(2,4)以原點為位似中心,將△ABC縮小后得到△DEF,若D(1,2),△DEF的面積為4,則△ABC的面積為( )A.2 B.4 C.8 D.16 組卷:654引用:13難度:0.9 -
 7.如圖,已知菱形ABCD的對角線AC、BD的長分別為6cm、8cm,AE⊥BC于點E,則AE的長是( )
7.如圖,已知菱形ABCD的對角線AC、BD的長分別為6cm、8cm,AE⊥BC于點E,則AE的長是( )A. 53cmB. 25cmC. 485cmD. 245cm組卷:2059引用:83難度:0.7 -
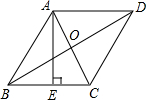
 8.如圖,正方形ABCD中,AB=6,點E在邊CD上,且CE=2DE.將△ADE沿AE對折至△AFE,延長EF交BC于點G,連結AG、BF、CF.下列結論:①△ABG≌△AFG;②FG=CG;③AG∥CF;④S△BFC=.其中正確結論的個數是( )365
8.如圖,正方形ABCD中,AB=6,點E在邊CD上,且CE=2DE.將△ADE沿AE對折至△AFE,延長EF交BC于點G,連結AG、BF、CF.下列結論:①△ABG≌△AFG;②FG=CG;③AG∥CF;④S△BFC=.其中正確結論的個數是( )365A.1個 B.2個 C.3個 D.4個 組卷:1339引用:10難度:0.2
三.解答題(共13小題,計81分,解答應寫出過程)
-
 25.一次函數y=x+2與反比例函數y=(x>0)在第一象限內交于點D.8x
25.一次函數y=x+2與反比例函數y=(x>0)在第一象限內交于點D.8x
(1)求點D的坐標;
(2)若點P是y軸上一點,在平面內是否存在點Q,使得以D,E,P,Q為頂點的四邊形是菱形?若存在,請求出點Q的坐標,若不存在,請說明理由.組卷:300引用:2難度:0.3 -
26.問題提出
(1)如圖1,在Rt△ABC中,∠ACB=90°,AC>BC,∠ACB的平分線交AB于點P,過點P分別作PE⊥AC,PF⊥BC.垂足分別為E,F,則圖1中四邊形PECF的形狀為 ;
問題探究
(2)如圖2,在Rt△ABC中,∠ACB=90°,AC=10,BC=6,∠ACB的平分線交AB于點P,過點P分別作PE⊥AC,PF⊥BC.垂足分別為E,F,求四邊形PECF的面積;
問題解決
(3)如圖3,△ABC是兒童公園內“少兒活動中心”的設計示意圖.已知AB=80m,∠ACB=120°,∠ACB的平分線交AB于點P,過點P分別作PE⊥AC,PF⊥BC,垂足分別為E,F.按設計要求,四邊形內部為室內活動區,陰影部分是室外活動區.若∠CAB=30°,求室內活動區PECF的面積.組卷:39引用:1難度:0.1


