2022-2023學(xué)年廣東省汕頭市潮南區(qū)兩英鎮(zhèn)八年級(jí)（下）期末數(shù)學(xué)試卷（A卷）

一．選擇題（共10小題，每題3分，共30分）

• 1．函數(shù)

  y

  =

  2022

  x

  中，自變量x的取值范圍是（　　）

  A．x＞0

  B．x＜0

  C．x≠0

  D．全體實(shí)數(shù)
  組卷：485引用：6難度：0.9

  解析

• 2．如果

  x

  -

  3

  是最簡(jiǎn)二次根式，則x的值可能是（　　）

  A．11

  B．13

  C．21

  D．27
  組卷：267引用：3難度：0.8

  解析

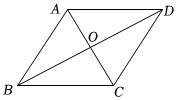• 3．如圖，四邊形ABCD是平行四邊形，其對(duì)角線AC，BD相交于點(diǎn)O，下列理論一定成立的是（　　）

  A．AC=BD

  B．AC⊥BD

  C．AB=CD

  D．AB=AD
  組卷：659引用：6難度：0.5

  解析

• 4．對(duì)于一組數(shù)據(jù)-1，-1，4，2，下列結(jié)論不正確的是（　　）

  A．平均數(shù)是1	B．眾數(shù)是-1
  C．中位數(shù)是0.5	D．方差是3.5
  組卷：886引用：17難度：0.9

  解析

• 5．當(dāng)

  x

  =

  23

  -

  1

  時(shí)，代數(shù)式x²+2x+2的值是（　　）

  A．23

  B．24

  C．25

  D．26
  組卷：1171引用：13難度：0.6

  解析

• 6．如圖，在Rt△ABC中，∠C=90°，AC=4，BC=3，分別以點(diǎn)A，B為圓心，以AB長(zhǎng)為半徑畫(huà)弧，兩弧相交于點(diǎn)D，連接AD，BD，則△ABD的周長(zhǎng)為（　　）

  A．9

  B．12

  C．6 3

  D．15
  組卷：497引用：5難度：0.8

  解析

• 7．如圖，在Rt△ABC中，∠ACB=90°，BD平分∠ABC，若CD=3，BC+AB=16，則△ABC的面積為（　　）

  A．6

  B．18

  C．24

  D．32
  組卷：471引用：2難度：0.6

  解析

五．解答題（共2小題，每題12分，共24分）

• 22．在平面直角坐標(biāo)系中，一次函數(shù)y=kx+5的圖象與x軸和y軸正半軸分別交于A，B兩點(diǎn)，且

  OB

  OA

  =

  1

  2

  ．
  （1）求一次函數(shù)y=kx+5的表達(dá)式；
  （2）若點(diǎn)P為該一次函數(shù)圖象上一點(diǎn)，且S_△POB=

  3

  2

  S_△AOB，求點(diǎn)P的坐標(biāo)．
  組卷：1635引用：2難度：0.5

  解析

• 23．如圖所示，在菱形ABCD中，AB=8，∠BAD=120°，△AEF為等邊三角形，點(diǎn)E、F分別在菱形的邊BC、CD上滑動(dòng)，且E、F不與B、C、D重合．
  （1）證明不論E、F在BC、CD上如何滑動(dòng)，總有BE=CF．
  （2）當(dāng)點(diǎn)E、F在BC、CD上滑動(dòng)時(shí)，分別探討四邊形AECF和△CEF的面積是否發(fā)生變化？如果不變，求出這個(gè)定值；如果變化，求出最大（或最小）值．
  組卷：476引用：6難度：0.6

  解析