2008年浙江省寧波市慈溪市七年級“數學應用與創新”競賽試卷

一、選擇題（共6小題，每小題4分，滿分24分）

• 1．杭州灣跨海大橋于5月1日23時58分開始試運行，大橋全長36千米，按規定橋上最低時速為60千米，最高時速為100千米，兩輛汽車從橋的南北兩端同時出發，正常行駛時到它們在途中交會所需時間可能為（　　）

  A．36分鐘

  B．22分鐘

  C．15分鐘

  D．7分鐘
  組卷：758引用：14難度：0.5

  解析

• 2．甲、乙兩袋裝有重量相等的大米（袋子還有較大的空余），先把甲袋的大米倒

  1

  3

  給乙袋，再把乙袋的大米倒

  3

  8

  給甲袋，結果（　　）

  A．甲袋多

  B．乙袋多

  C．一樣多

  D．誰多誰少，要視原來每袋大米的重量而定
  組卷：803引用：5難度：0.5

  解析

• 3．如圖，一張紙的厚度為0.07mm,連續對折15次，這時它的厚度最接近于（　　）

  A．數學課本的厚度	B．書桌的高度
  C．姚明的身高	D．三層樓的高度
  組卷：405引用：15難度：0.5

  解析

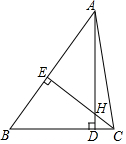• 4．如圖，在△ABC中AD⊥BC，CE⊥AB，垂足分別為D、E，AD、CE交于點H，已知EH=EB=3，AE=4，則CH的長是（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：4145引用：77難度：0.9

  解析

• 5．已知三角形的每條邊長都是整數，且均不大于4，這樣的互不全等的三角形有（　　）

  A．9個

  B．11個

  C．12個

  D．13個
  組卷：137引用：4難度：0.9

  解析

• 6．現有一個長方體水箱，從水箱里面量得它的深是30cm,底面的長是25cm,寬是20cm.水箱里盛有深為acm（0＜a≤8）的水，若往水箱里放入棱長為10cm的立方體鐵塊，則此時水深為（　　）

  A． 4 3 a cm

  B． 5 4 a cm

  C．（a+2）cm

  D． 5 a + 10 6 cm
  組卷：240引用：3難度：0.9

  解析

三、解答題（共4小題，滿分46分）

• 19．已知a、b、c為正整數，且a²+b²=c²，又a為質數．說明下列結論成立的理由：（1）b、c兩數必為一奇一偶；（2）2（a+2b-c+2）是完全平方數（即一個正整數的平方）
  組卷：57引用：2難度：0.5

  解析

• 20．甲、乙、丙三人分小球，分法如下：先在三張紙簽上各寫上三個正整數a、b、c,使a＜b＜c.分小球時，每人抽一張簽，然后把抽得的簽上的數減去a,所得結果就是他這一輪分得的小球個數，以后重復上述過程（每次寫上的數不變）．經過若干輪（不小于2輪）這種分法后，甲共得到了20個小球，乙共得10個小球，丙共得9個小球，又知最后一次乙拿到的紙簽上寫的數是c,而丙在各輪中拿到的紙簽上寫的數字之和是18，問正整數a、b、c各是多少？為什么？
  組卷：100引用：2難度：0.3

  解析