2022-2023學年重慶市忠縣后鄉三校八年級（下）期中數學試卷

一、選擇題：（本大題10個小題，每小題4分，共40分）在每個小題的下面，都給出了代號為A、B、C、D的四個答案，其中只有一個是正確的，請將答題卡上題號右側正確答案所對應的方框涂黑.

• 1．2的相反數是（　　）

  A． 1 2

  B．- 1 2

  C．2

  D．-2
  組卷：780引用：90難度：0.9

  解析

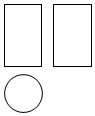• 2．如圖是一個幾何體的三視圖，該幾何體是（　　）

  A．球

  B．圓錐

  C．圓柱

  D．棱柱
  組卷：973引用：13難度：0.8

  解析

• 3．已知a＞b,下列不等式的變形不正確的是（　　）

  A．a-1＞b-1

  B．a-c＞b-c

  C．2a＞2b

  D．ac＞bc
  組卷：328引用：7難度：0.8

  解析

• 4．三角形的三邊分別為a、b、c,由下列條件不能判斷它是直角三角形的是（　　）

  A．a：b：c=13：5：12	B．a= 1 3 ，b= 1 4 ，c= 1 5
  C．a2=（b+c）（b-c）	D．a2-b2=c2
  組卷：203引用：1難度：0.8

  解析

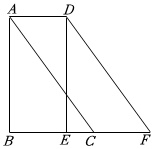• 5．如圖，在Rt△ABC中，∠B=90°，AB=4，將Rt△ABC沿BC向右平移得到△DEF，若四邊形ACFD的面積等于8，則平移的距離等于（　　）

  A．2

  B．3

  C． 2 3

  D．4
  組卷：182引用：2難度：0.7

  解析

• 6．按如圖所示的運算程序，能使輸出的結果為4的是（　　）
  

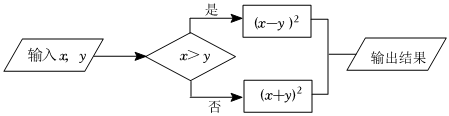
  A．x=1，y=2

  B．x=2，y=1

  C．x=3，y=1

  D．x=2，y=3
  組卷：207引用：6難度：0.7

  解析

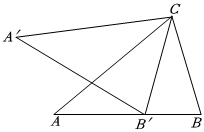• 7．如圖，將△ABC繞點C順時針旋轉后得到△A′B′C，且點B′恰好落在邊AB上，若∠B=α，則∠A′CA=（　　）

  A． 1 2 α

  B．α

  C．90°-α

  D．180°-2α
  組卷：320引用：2難度：0.5

  解析

• 8．將一些完全相同的梅花按如圖所示的規律擺放，第1個圖形有5朵梅花，第2個圖形有8朵梅花，第3個圖形有13朵梅花，?，按此規律，則第6個圖形中共有梅花的朵數是（　　）
  

  A．39

  B．40

  C．41

  D．42
  組卷：46引用：2難度：0.6

  解析

三、解答題：（本大題8個小題，19題8分，20-26每小題8分，共78分）解答時每小題必須給出必要的演算過程或推理步驟，畫出必要的圖形（包括輔助線），請將解答過程書寫在答題卡中對應的位置上.

• 25．如圖，拋物線y=-x²+bx+c與x軸交于點A（-3，0），點B（1，0），與y軸相交于點C．
  （1）求拋物線的函數表達式；
  （2）點P是第二象限內拋物線上一動點，連接AC，D是線段AC的中點，連接AP，DP，求△APD面積的最大值及此時點P的坐標；
  （3）在（2）中，△APD面積的取最大值的條件下，將原拋物線沿射線AC的方向平移2

  2

  個單位長度，得到新拋物線y₁．點M為新拋物線y₁對稱軸上一點，點N為平面內一點，若以A，P，M，N為頂點的四邊形是矩形，直接寫出所有符合條件的點N的坐標，并選擇其中一個寫出求解過程．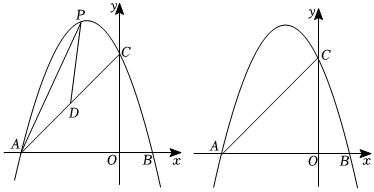
  
  組卷：415引用：2難度：0.1

  解析

• 26．如圖1，△ABC中，AC=BC，點D是線段AC上任意一點，連接BD．
  （1）如圖1，若∠ACB=90°，過點C作CE⊥BD于點E，連接AE，若AD：CD=3：2，CE=2，求AE．
  （2）如圖2，點E在線段BC上，連接AE，點F在線段AE上，點G是線段DB的中點，連接DF，FG．若∠ACB=∠EFD，∠AEB=3∠FAD，求證：FG⊥CG．
  （3）如圖3，若∠CDB=60°，點N是射線DB上的動點，點M是射線DC上的動點，點P是平面上任意一點，連接PM，PN，MN，PM=PN，且∠MPN=120°，當線段DP的距離最大時，連接AP，AN，若∠NAM=45°，線段MN的長為4，直接寫出△PAN的面積．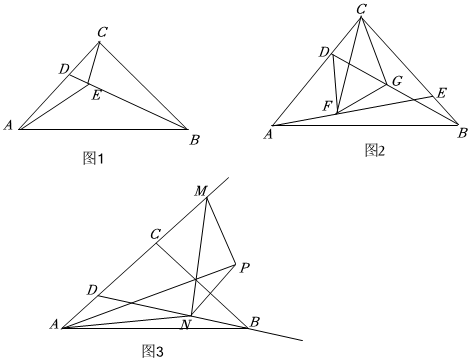
  
  組卷：221引用：1難度：0.1

  解析