2014-2015學年江蘇省揚州市江都區宜陵中學八年級（上）數學周練試卷（8）

一、選擇題

• 1．下列各組數中，不能作為直角三角形三邊長的是（　　）

  A．9，12，15

  B．7，24，25

  C．3，4，5

  D．3，5，7
  組卷：63引用：3難度：0.9

  解析

• 2．

  4

  的平方根是（　　）

  A．2

  B．±2

  C． 2

  D．± 2
  組卷：2713引用：244難度：0.9

  解析

• 3．下列說法中不正確的是（　　）

  A．-2是4的平方根

  B． 3 8 是8的立方根

  C．立方根等于它本身的數只有1和0

  D．平方根等于它本身的數只有0
  組卷：64引用：3難度：0.9

  解析

• 4．下列無理數有（　　）個
  

  22

  7

  ，

  3

  ，

  3

  8

  ，

  4

  ，

  π

  3

  ，0.1，-0.010010001…，-5．

  A．1

  B．2

  C．3

  D．4
  組卷：43引用：1難度：0.9

  解析

• 5．如圖一直角三角形紙片，兩直角邊AC=3cm,BC=4cm,現將直角邊AC沿直線AD折疊，使它落在斜邊AB上，且與AE重合，則CD等于（　　）

  A．2cm

  B．3cm

  C．1.5cm

  D．4cm
  組卷：78引用：3難度：0.7

  解析

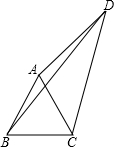• 6．如圖，四邊形ABCD中，AC，BD是對角線，△ABC是等邊三角形．∠ADC=30°，AD=3，BD=5，則CD的長為（　　）

  A． 3 2

  B．4

  C． 2 5

  D．4.5
  組卷：3322引用：18難度：0.7

  解析

• 7．如圖，設正方體ABCD-A₁B₁C₁D₁的棱長為1，黑、白兩個甲殼蟲同時從A點出發，以相同的速度分別沿棱向前爬行，黑甲殼蟲爬行的路線是AA₁→A₁D₁→…，白甲殼蟲爬行的路線是AB→BB₁→…，并且都遵循如下規則：所爬行的第n+2與第n條棱所在的直線必須是既不平行也不相交（其中n是正整數）．那么當黑、白兩個甲殼蟲各爬行完第2013條棱分別停止在所到的正方體頂點處時，它們之間的距離是（　　）

  A．0

  B．1

  C． 2

  D． 3
  組卷：293引用：4難度：0.9

  解析

四、解答題（共6小題，滿分10分）

• 20．如圖，C為線段BD上一動點，分別過點B、D作AB⊥BD，ED⊥BD，連接AC、EC．已知AB=5，DE=2，BD=12，設CD=x.
  （1）用含x的代數式表示AC+CE的長；
  （2）請問點C在BD上什么位置時，AC+CE的值最小？
  （3）根據（2）中的規律和結論，請構圖求出代數式

  x

  2

  +

  9

  +

  （

  24

  -

  x

  ）

  2

  +

  16

  的最小值．
  組卷：1038引用：7難度：0.1

  解析

• 21．閱讀理解題：
  【幾何模型】條件：如圖1，A、B是直線l同旁的兩個定點．
  問題：在直線l上確定一點P，使PA+PB的值最小．
  方法：作點A關于直線l的對稱點A′，連接A′B交l于點P，則PA+PB=A′P+PB=A′B，
  由“兩點之間，線段最短”可知，點P即為所求的點．
  【模型應用】
  （1）如圖2，正方形ABCD的邊長為2，E為AB的中點，P是AC上一動點．求出PB+PE的最小值（畫出示意圖，并解答）
  （2）如圖3，∠AOB=45°，P是∠AOB內一定點，PO=10，Q、R分別是OA、OB上的動點，求△PQR周長的最小值．（要求畫出示意圖，寫出解題過程）
  
  組卷：289引用：1難度：0.3

  解析