當前位置：試卷中心 > 試卷詳情

2022-2023學年甘肅省武威市民勤一中高一（下）第二次月考數學試卷

發布：2024/5/24 8:0:9

1．復數z=（3-2i）（2+3i）的共軛復數
z
=（　　）
A．12+5i B．12-5i C．5i D．-5i
組卷：20引用：3難度：0.8
解析
2．已知向量
a
=
（
2
，
1
）
，
b
=
（
x
,-
2
）
，若
a
∥
b
，則
a
+
b
=（　　）
A．（-2，-1） B．（2，1） C．（3，-1） D．（-3，1）
組卷：473引用：14難度：0.9
解析
3．在△ABC中，已知A=60°，BC=4，則△ABC的外接圓半徑為（　　）
A．4
3
B．4 C．
4
3
3
D．
8
3
3
組卷：306引用：5難度：0.9
解析
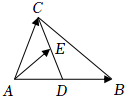4．如圖，在△ABC中，D為AB的中點，E為CD的中點，設
AB
=
a
，
AC
=
b
，以向量
a
，
b
為基底，則向量
AE
=（　　）
A．
1
2
a
+
b
B．
1
4
a
+
1
2
b
C．
a
+
1
2
b
D．
1
2
a
+
1
4
b
組卷：472引用：10難度：0.7
解析
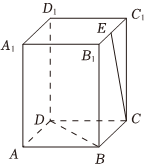5．如圖，在長方體ABCD-A₁B₁C₁D₁中，已知AB=BC=2，AA₁=5，E為B₁C₁的中點，則異面直線BD與CE所成角的余弦值為（　　）
A．
5
10
B．
34
34
C．
13
26
D．
13
13
組卷：490引用：8難度：0.7
解析
6．如圖所示，在三棱臺A′B′C′-ABC中，沿A′BC截去三棱錐A′-ABC，則剩余的部分是（　　）
A．三棱錐 B．四棱錐 C．三棱柱 D．組合體
組卷：1481引用：23難度：0.9
解析
7．已知向量
a
，
b
的夾角為
5
π
6
，且
|
a
|
=
2
3
，
b
=
（
-
3
，
4
）
，則
|
a
+
2
b
|
=（　　）
A．172 B．
43
C．
2
13
D．20
組卷：61引用：2難度：0.7
解析

21．在△ABC中，角A，B，C所對的邊分別a,b,c,且bcosA+acosB=2ccosA．
（1）求角A的值；
（2）已知D在邊BC上，且BD=3DC，AD=3，求△ABC的面積的最大值．
組卷：678引用：9難度：0.5
解析
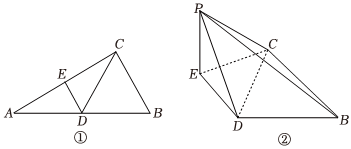22．在△ABC中，D，E分別為AB，AC的中點，AB=2BC=2CD，如圖①，以DE為折痕將△ADE折起，使點A到達點P的位置，如圖②．
（1）證明：CP⊥DE；
（2）若CE⊥平面DEP，且AB=2，求點C到平面PBD的距離．
組卷：50引用：6難度：0.5
解析

1．復數z=（3-2i）（2+3i）的共軛復數z=（ ）