2022-2023學年重慶市兼善中學優質教育集團九年級（下）期中數學試卷

一、選擇題：（本大題10個小題，每小題4分，共40分）

• 1．-2的相反數是（　　）

  A．2

  B．-2

  C． - 1 2

  D． 1 2
  組卷：4758引用：1083難度：0.9

  解析

• 2．下列圖形中，不是軸對稱圖形的是（　　）

  A．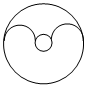

  B．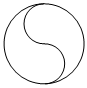

  C．

  D．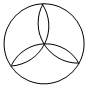
  組卷：43引用：3難度：0.9

  解析

• 3．如圖所示，下列條件中能說明a∥b的是（　　）

  A．∠1=∠2

  B．∠3=∠4

  C．∠2+∠4=180°

  D．∠1+∠4=180°
  組卷：951引用：13難度：0.7

  解析

• 4．小玲從山腳沿某上山步道“踏青”，勻速行走一段時間后到達山腰平臺停下來休息一會兒，休息結束后她加快了速度，勻速直至到達山頂．設從她出發開始所經過的時間為t,她行走的路程為s,下面能反映s與t的函數關系的大致圖象是（　　）

  A．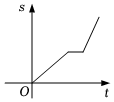

  B．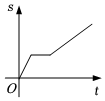

  C．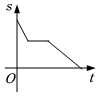

  D．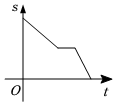
  組卷：234引用：5難度：0.7

  解析

• 5．用大小相同的圓點擺成如圖所示的圖案，按照這樣的規律擺放，則第10個圖案中共有圓點的個數是（　　）
  

  A．71

  B．70

  C．65

  D．59
  組卷：265引用：8難度：0.7

  解析

• 6．估計（

  3

  +3

  2

  ）×

  1

  3

  的值應在（　　）

  A．2和3之間

  B．3和4之間

  C．4和5之間

  D．5和6之間
  組卷：19引用：2難度：0.9

  解析

• 7．國家實施“精準扶貧”政策以來，很多貧困人口走向了致富的道路，某地區2019年底有貧困人口9萬人，通過社會各界的努力，2021年底貧困人口減少至1萬人．設2019年底至2021年底該地區貧困人口的年平均下降率為x,根據題意列方程得（　　）

  A．9（1-2x）=1

  B．9（1-x）2=1

  C．9（1+2x）=1

  D．9（1+x）2=1
  組卷：32引用：2難度：0.8

  解析

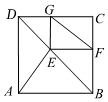• 8．如圖所示，E是正方形ABCD的對角線BD上一點，EF⊥BC，EG⊥CD，垂足分別是F、G，若CG=4，CF=3，則AE的長是（　　）

  A．3

  B．4

  C．5

  D．7
  組卷：1142引用：8難度：0.6

  解析

四、解答題：（本大題共6個小題，每小題10分，共60分）

• 25．如圖，在平面直角坐標系中，拋物線

  y

  =

  -

  1

  2

  x

  2

  +

  bx

  +

  c

  與x軸交于A（-2，0）、B（4，0）兩點（點A在點B的左側），與y軸交于點C，連接AC、BC，點P為直線BC上方拋物線上一動點，連接OP交BC于點Q．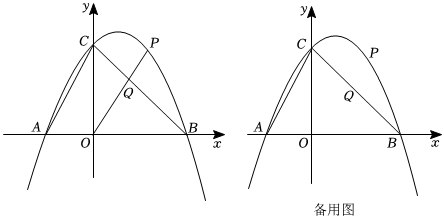
  
  （1）求拋物線的函數表達式；
  （2）當

  PQ

  OQ

  的值最大時，求點P的坐標和

  PQ

  OQ

  的最大值；
  （3）把拋物線

  y

  =

  -

  1

  2

  x

  2

  +

  bx

  +

  c

  向右平移1個單位，再向上平移2個單位得新拋物線y'，M是新拋物線上一點，N是新拋物線對稱軸上一點，當以M、N、B、C為頂點的四邊形是平行四邊形時，寫出所有符合條件的N點的坐標，并寫出求解點N的坐標的其中一種情況的過程．
  組卷：414引用：1難度：0.2

  解析

• 26．已知正方形ABCD的邊長為4，△BEF為等邊三角形，點E在AB邊上，點F在AB邊的左側．
  （1）如圖1，若D，E，F在同一直線上，求BF的長；
  （2）如圖2，連接AF，CE，BD，并延長CE交AF于點H，若CH⊥AF，求證：

  2

  AE+2FH=BD；
  （3）如圖3，將△ABF沿AB翻折得到△ABP，點Q為AP的中點，連接CQ，若點E在射線BA上運動時，請直接寫出線段CQ的最小值．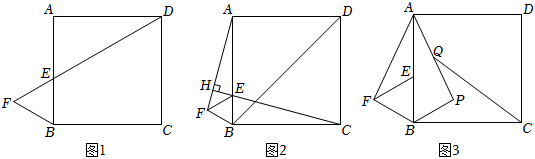
  
  組卷：1044引用：10難度：0.2

  解析