當前位置：試卷中心 > 試卷詳情

2022-2023學年北京大學附中行知學院高一（下）期中數學試卷

發布：2024/12/5 6:30:2

一、選擇題共10小題，每小題4分，共40分.在每小題列出的四個選項中，選出符合題目要求的一項.

1．已知點（1，2）在α的終邊上，則cosα=（　　）
A．
2
5
5
B．
5
5
C．
2
3
D．
1
3
組卷：228引用：4難度：0.8
解析
2．將α的終邊逆時針旋轉30°，與120°的終邊重合，則與α終邊相同的角的集合為（　　）
A．{β|β=k×180°+90°，k∈Z} B．{β|β=k×360°+90°，k∈Z}
C．{β|β=k×180°+150°，k∈Z} D．{β|β=k×360°+150°，k∈Z}
組卷：369引用：2難度：0.7
解析
3．已知sinα＜0，且tanα＞0，則α的終邊所在的象限是（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
組卷：820引用：5難度：0.9
解析
4．已知tanα=2，則
cosα
+
3
sinα
3
cosα
-
sinα
=（　　）
A．7 B．
7
5
C．1 D．
5
7
組卷：266引用：2難度：0.9
解析
5．已知α是第二象限角，若sin（
π
2
-α）=-
1
3
，則sinα=（　　）
A．
-
2
2
3
B．
-
1
3
C．
1
3
D．
2
2
3
組卷：958引用：7難度：0.8
解析
6．已知非零向量
OA
，
OB
不共線，且
BM
=
1
3
BA
，則向量
OM
=（　　）
A．
1
3
OA
+
2
3
OB
B．
2
3
OA
+
1
3
OB
C．
1
3
OA
-
2
3
OB
D．
2
3
OA
-
1
3
OB
組卷：155引用：2難度：0.9
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題共4小題，共40分。解答應寫出文字說明、演算步橾或證明過程。

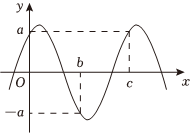18．已知函數f（x）=Asin（ωx+φ）（A＞0，ω＞0，
|
φ
|
＜
π
2
）的部分圖象如圖所示．
（1）若c=π，則ω=____；
（2）在條件①、條件②、條件③、條件④這四個條件中選擇三個作為已知，使A，ω，φ唯一確定．則選擇的三個條件序號可以是_____，此時A=_____，ω=_____，φ=_____；
（3）利用（2）中的結論，設g（x）=f（2x），若函數g（x）在區間[0，m]上單調遞增，求實數m的最大值．
條件①：
a
=
3
；條件②：b=2；
條件③：c=3；條件④：f（9）=1．
注：如果選擇的條件不符合要求，第（3）問得0分．
組卷：97引用：2難度：0.6
解析
19．有如下條件：①對?x_i∈（0，t），i=1，2，x₁＜x₂，均有f（x₁）＜f（x₂）；
②對?x_i∈（0，t），i=1，2，x₁＜x₂，均有f（x₁）＞f（x₂）；
③對?x_i∈（0，t），i=1，2，3，x₁+x₂+x₃=π；若x₁＜x₂＜x₃，則均有f（2x₁）＜f（2x₂）＜f（2x₃）；
④對?x_i∈（0，t），i=1，2，3，x₁+x₂+x₃=π；若x₁＜x₂＜x₃，則均有f（2x₁）＞f（2x₂）＞f（2x₃）．
（1）設函數f（x）=sinx,
t
=
π
2
，直接寫出該函數滿足的所有條件序號；
（2）設
x
∈
（
0
，
π
4
）
，比較函數f（x）=（sinx）^cosx，g（x）=（cosx）^sinx，h（x）=（sinx）^sinx，g（x）=（cosx）^sinx，h（x）=（sinx）^sinx值的大小，并說明理由；
（3）設函數
f
（
x
）
=
sinx
x
，滿足條件②，求證：t的最大值t_max≥π．（注：導數法不予計分）
組卷：41引用：3難度：0.6
解析