2022-2023學年上海市閔行區七寶中學高二（上）期末數學試卷

一、填空題（1-6題每題4分，7-12題每題5分）

• 1．直線4x+3y-5=0的一個法向量為

  ．
  組卷：80引用：1難度：0.8

  解析

• 2．若a是4+m,4-m的等差中項，則a=

  ．
  組卷：259引用：1難度：0.8

  解析

• 3．以點（3，4）為圓心，且經過原點的圓的方程為

  ．
  組卷：332引用：2難度：0.8

  解析

• 4．雙曲線

  y

  2

  4

  -

  x

  2

  16

  =

  1

  的離心率為

  ．
  組卷：100引用：1難度：0.8

  解析

• 5．過點（0，4）作直線與拋物線y²=x有且僅有一個交點，這樣的直線可以作出

  條．
  組卷：111引用：1難度：0.6

  解析

• 6．直線l₁：x-3y+3=0與直線l₂：x+y=0的夾角記為θ，則cosθ=

  ．
  組卷：73引用：1難度：0.8

  解析

• 7．已知集合M={（x,y）|x²+y²≤4}與N={（x-1）²+（y-1）²≤r²，r＞0}滿足M∩N=N，則r的取值范圍是
  組卷：65引用：1難度：0.7

  解析

三、解答題

• 20．已知雙曲線

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的左、右焦點分別為F₁、F₂，直線l過右焦點F₂且與雙曲線C交于A、B兩點．
  （1）若雙曲線C的離心率為

  3

  ，虛軸長為

  2

  2

  ，求雙曲線C的焦點坐標；
  （2）設a=1，

  b

  =

  3

  ，若l的斜率存在，且

  （

  F

  1

  A

  +

  F

  1

  B

  ）

  ?

  AB

  =

  0

  ，求l的斜率；
  （3）設l的斜率為

  3

  5

  ，

  |

  OA

  +

  OB

  |

  =

  |

  OA

  -

  OB

  |

  =

  4

  ，求雙曲線C的方程．
  組卷：340引用：7難度：0.6

  解析

• 21．已知橢圓方程為

  x

  2

  4

  +

  3

  y

  2

  4

  =

  1

  ，左右焦點分別為F₁，F₂，A（2，0）是長軸的右端點．點C在橢圓上，C關于原點的對稱點為B．過C作直線l垂直于x軸，與x軸相交于M．
  （1）當C為橢圓的上頂點時，求三角形F₁F₂C的周長（直接寫出結果）；
  （2）若C在第一象限，且直線BM與直線AC的斜率乘積為

  -

  1

  2

  ，求tan∠BAC；
  （3）在（2）的條件下，設，PQ是橢圓上位于第四象限的兩點（Q在P的右邊），直線l與線段PQ相交于N，且滿足|PN|?|QC|=|PC|?|QN|．判斷四邊形AQPB的形狀，并說明理由．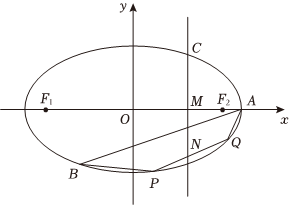
  
  組卷：100引用：1難度：0.4

  解析