2022年遼寧省縣級重點高中協作體高考數學一模試卷

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．在復平面內，復數Z和Z₁=

  2

  i

  1

  -

  i

  （i為虛數單位）表示的點關于虛軸對稱，則復數Z=（　　）

  A．-1+i

  B．1+i

  C．-1-i

  D．1-i
  組卷：80引用：2難度：0.8

  解析

• 2．已知集合A={x|-x²-2x+8＜0}，B={x|x＜a}，若A∪B=R，則實數a的取值范圍為（　　）

  A．[-4，+∞）

  B．（-4，+∞）

  C．[2，+∞）

  D．（2，+∞）
  組卷：92引用：1難度：0.8

  解析

• 3．已知曲線

  C

  ：

  x

  2

  4

  a

  +

  y

  2

  3

  a

  +

  2

  =

  1

  ，則“a＞0”是“曲線C是橢圓”的（　　）

  A．充要條件	B．充分不必要條件
  C．必要不充分條件	D．既不充分也不必要條件
  組卷：181引用：5難度：0.8

  解析

• 4．在我國瓷器的歷史上六棱形的瓷器非常常見，因為六、八是中國人的吉利數字，所以許多瓷器都做成六棱形和八棱形的，但是六棱柱形的瓷器只有六棱柱形筆筒，其余的六棱形都不是六棱柱形．如圖為一個正六棱柱形狀的瓷器筆筒，高為18.7cm,底面邊長為7cm（數據為筆筒的外觀數據），用一層絨布將其側面包裹住，忽略絨布的厚度，則至少需要絨布的面積為（　　）

  A．120cm2

  B．162.7cm2

  C．785.4cm2

  D．1570.8cm2
  組卷：119引用：1難度：0.7

  解析

• 5．函數

  y

  =

  cosx

  x

  的圖象大致為（　　）

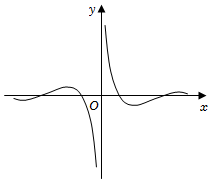
  A．	B．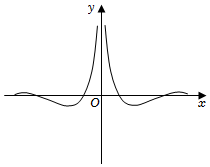
  C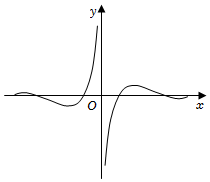．	D．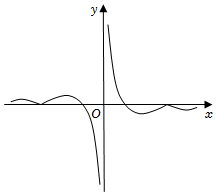
  組卷：82引用：2難度：0.6

  解析

• 6．習近平主席“綠水青山就是金山銀山”的反復叮嚀，人們已經耳熟能詳，由此帶來的發展方式轉化，實實在在地改變著中國的樣貌．某工廠產生的廢氣必須經過過濾后排放，規定排放時污染物的殘留含量不得超過原污染物總量的0.25%．已知在過濾過程中的污染物的殘留數量P（單位：毫克/升）與過濾時間t（單位：小時）之間的函數關系為

  P

  =

  P

  0

  ?

  e

  kt

  （其中e是自然對數的底數，k為常數，P₀為原污染物總量）．若前4個小時廢氣中的污染物被過濾掉了80%，則要能夠按規定排放廢氣，還需要過濾n小時，則正整數n的最小值為（　　）（參考數據：log₅2≈0.43）

  A．9

  B．11

  C．13

  D．15
  組卷：57引用：3難度：0.7

  解析

• 7．將函數f（x）=sinωx（ω＞0）圖像上所有點的橫坐標縮短到原來的

  1

  2

  倍（縱坐標不變），再向左平移

  π

  8

  ω

  個單位長度，得到函數g（x）的圖像，若g（x）在（

  π

  2

  ，π）上單調遞減，則實數ω的取值范圍為（　　）

  A．（0， 1 4 ]

  B．（0， 5 8 ]

  C．[ 1 4 ， 5 4 ]

  D．[ 1 4 ， 5 8 ]
  組卷：980引用：2難度：0.5

  解析

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

• 21．已知拋物線C：y²=2px（p＞0）的焦點為F，過點（m,0）且斜率為k的直線l與拋物線C交于A，B兩點．
  （1）當k=2且p=2m時，|AB|=15，求拋物線C的方程；
  （2）已知橫坐標為-

  p

  2

  的點D在直線l上，若對任意正數m,

  FA

  ?

  FB

  =|FD|²?cos∠AFB恒成立，求k的值．
  組卷：81引用：3難度：0.4

  解析

• 22．已知函數f（x）=xlnx-ax³-x,a∈R．
  （1）若f（x）存在單調遞增區間，求a的取值范圍；
  （2）若x₁，x₂（x₁＜x₂）是f（x）的兩個不同極值點，證明：3lnx₁+lnx₂＞1．
  組卷：343引用：5難度：0.4

  解析