當前位置：試卷中心 > 試卷詳情

2022-2023學年安徽省江南十校高二（下）聯考數學試卷（5月份）

發布：2024/7/5 8:0:9

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．過點（1，3）且與直線2x+y-6=0平行的直線方程為（　　）
A．2x+y-5=0 B．2x+y+5=0 C．x-2y+5=0 D．x-2y-5=0
組卷：158引用：2難度：0.8
解析
2．已知隨機變量X～N（μ，σ²），其正態曲線如圖所示，若P（10＜X＜30）=m（0＜m＜1），則P（X≥30）=（　　）
A．1-m B．
m
2
C．
m
+
1
2
D．
1
-
m
2
組卷：46引用：2難度：0.8
解析
3．我國古代數學家提出的“中國剩余定理”又稱“孫子定理”，它是世界數學史上光輝的一頁，定理涉及的是整除問題．現有如下一個整除問題：將1至2023這2023個數中，能被3除余1且被5除余2的數按從小到大的順序排成一列，構成數列{a_n}，則此數列的項數為（　　）
A．133項 B．134項 C．135項 D．136項
組卷：49引用：2難度：0.7
解析
4．圓C₁：x²+y²-6x-7=0與圓C₂：x²+y²+2
7
y+6=0的位置關系是（　　）
A．外離 B．外切 C．相交 D．內切
組卷：253引用：2難度：0.8
解析
5．隨機變量X，Y滿足X+2Y=1，且Y～B（4，0.5），則E（X）與D（X）的值分別為（　　）
A．-3，4 B．3，4 C．4，3 D．4，-3
組卷：51引用：3難度：0.7
解析
6．2023年亞運會于2023年9月23日至10月8日在中國浙江杭州舉行，杭州亞運會吉祥物是一組承載深厚底蘊和充滿活力的機器人，組合名為“江南憶”，出自唐朝詩人白居易的名句“江南憶，最憶是杭州”，融合了杭州的歷史人文、自然生態和創新基因．現將編號為1-6的6個吉祥物機器人贈送給3名亞運會志愿者留作紀念，若要求每名志愿者至少獲得1個吉祥物且1號和2號吉祥物被贈送給同一名志愿者，則不同的贈送方法數為（　　）
A．36 B．72 C．114 D．150
組卷：67引用：3難度：0.5
解析
7．如圖，三棱錐A-BCD中，AB、CD所成的角為α，則（　　）
A．
cosα
=
|
|
BD
|
2
+
|
BC
|
2
+
|
AD
|
2
-
|
AC
|
2
|
2
|
AB
|
|
CD
|
B．
cosα
=
|
|
AD
|
2
+
|
BC
|
2
-
|
BD
|
2
-
|
AC
|
2
|
2
|
AB
|
|
CD
|
C．
cosα
=
|
|
AC
|
2
+
|
BC
|
2
+
|
BD
|
2
-
|
AD
|
2
|
2
|
AB
|
|
CD
|
D．
cosα
=
|
|
BC
|
2
+
|
BD
|
2
-
|
AD
|
2
-
|
AC
|
2
|
2
|
AB
|
|
CD
|
組卷：31引用：2難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分.解答應寫出必要的文字說明、證明過程及演算步驟.

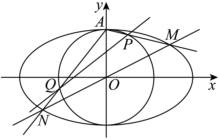21．如圖，點A為橢圓
Γ
：
x
2
4
+
y
2
=
1
的上頂點，圓C：x²+y²=1，過坐標原點O的直線l交橢圓Γ于M，N兩點．
（1）求直線AM，AN的斜率之積；
（2）設直線AM：y=kx+1（k≠0），AN與圓C交于P，Q兩點，記直線MN，PQ的斜率分別為k₁，k₂，探究是否存在實數λ，使得k₁=λk₂？若存在，求出λ的值；若不存在，請說明理由．
組卷：78引用：2難度：0.2
解析
22．已知函數f（x）=lnx-1+
1
x
，
g
（
x
）
=
2
ax
+
1
2
x
2
，其中a∈R．
（1）求函數f（x）的最小值；
（2）若h（x）=4f（x）+4-
4
x
+g（x）有兩個極值點x₁，x₂（x₁＜x₂），求實數a的取值范圍，并證明：-x₁-
8
x
2
1
＜
h
（
x
2
）
＜
-
6
+
4
ln
2
..
組卷：31引用：3難度：0.3
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

2022-2023學年安徽省江南十校高二（下）聯考數學試卷（5月份）

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．過點（1，3）且與直線2x+y-6=0平行的直線方程為（ ）

2．已知隨機變量X～N（μ，σ2），其正態曲線如圖所示，若P（10＜X＜30）=m（0＜m＜1），則P（X≥30）=（ ）

4．圓C1：x2+y2-6x-7=0與圓C2：x2+y2+27y+6=0的位置關系是（ ）

5．隨機變量X，Y滿足X+2Y=1，且Y～B（4，0.5），則E（X）與D（X）的值分別為（ ）

7．如圖，三棱錐A-BCD中，AB、CD所成的角為α，則（ ）

四、解答題：本題共6小題，共70分.解答應寫出必要的文字說明、證明過程及演算步驟.

22．已知函數f（x）=lnx-1+1x，g（x）=2ax+12x2，其中a∈R．（1）求函數f（x）的最小值；（2）若h（x）=4f（x）+4-4x+g（x）有兩個極值點x1，x2（x1＜x2），求實數a的取值范圍，并證明：-x1-8x21＜h（x2）＜-6+4ln2..

1．過點（1，3）且與直線2x+y-6=0平行的直線方程為（　　）

2．已知隨機變量X～N（μ，σ²），其正態曲線如圖所示，若P（10＜X＜30）=m（0＜m＜1），則P（X≥30）=（　　）

4．圓C₁：x²+y²-6x-7=0與圓C₂：x²+y²+2
7
y+6=0的位置關系是（　　）

5．隨機變量X，Y滿足X+2Y=1，且Y～B（4，0.5），則E（X）與D（X）的值分別為（　　）

7．如圖，三棱錐A-BCD中，AB、CD所成的角為α，則（　　）