2023年廣東省深圳市福田區(qū)中考數(shù)學(xué)二模試卷
發(fā)布：2024/4/20 14:35:0
一、選擇題（本大題共10小題，每小題3分，共30分，每小題有四個(gè)選項(xiàng)，其中只有一個(gè)是正確的）
-
1．如圖，數(shù)軸上點(diǎn)A表示的數(shù)的相反數(shù)是（ ）組卷：270引用：3難度：0.9 -
2．如圖，是由相同大小的五個(gè)小正方體組成的立體模型，它的俯視圖是（ ）組卷：162引用：5難度：0.8 -
3．位于深圳市光明中心區(qū)科學(xué)公園的深圳科技館占地面積為66000m2．66000用科學(xué)記數(shù)法可以表示成（ ）
組卷：99引用：3難度：0.8 -
4．不等式組
的解集是（ ）x-1＞1-2x≤2組卷：380引用：2難度：0.7 -
5．下列計(jì)算正確的是（ ）
組卷：196引用：1難度：0.7 -
6．觀察下列尺規(guī)作圖痕跡，其中所作線段AD為△ABC的角平分線的是（ ）
組卷：504引用：3難度：0.6 -
7．為響應(yīng)“雙減”政策，進(jìn)一步落實(shí)“立德樹人、五育并舉”的思想主張，深圳某學(xué)校積極推進(jìn)學(xué)生綜合素質(zhì)評(píng)價(jià)改革，小芳在本學(xué)期德、智、體、美、勞的評(píng)價(jià)得分如圖所示，其各項(xiàng)的得分分別為9，8，10，8，7，則該同學(xué)這五項(xiàng)評(píng)價(jià)得分的眾數(shù)，中位數(shù)，平均數(shù)分別為（ ）組卷：387引用：4難度：0.6
三、解答題（本題共7小題，其中第16題5分，第17題7分，第18題8分，第19題8分，第20題8分，第21題9分，第22題10分，共55分）
-
21．【綜合與實(shí)踐】我國海域的島嶼資源相當(dāng)豐富，總面積達(dá)72800多平方公里，有人居住的島嶼達(dá)450個(gè)．位于北部灣的某小島，外形酷似橄欖球，如圖1所示．
如圖2所示，現(xiàn)把海岸線近似看作直線m,小島面對(duì)海岸線一側(cè)的外緣近似看作AB，經(jīng)測量，AB的長可近似為250π海里，它所對(duì)的圓心角（∠AOB）的大小可近似為90°．（注：AB在m上的正投影為圖中線段CD，點(diǎn)O在m上的正投影落在線段CD上．）
（1）求的半徑r；?AB
（2）因該島四面環(huán)海，淡水資源缺乏，為解決島上居民飲用淡水難的問題，擬在海岸線上，建造一個(gè)淡水補(bǔ)給站，向島上居民輸送淡水．為節(jié)約運(yùn)輸成本，要求補(bǔ)給站到小島外緣AB的距離最近（即，要求補(bǔ)給站與上的任意一點(diǎn)，兩點(diǎn)之間的距離取得最小值．）；?AB
請你依據(jù)所學(xué)幾何知識(shí)，在圖2中畫出補(bǔ)給站位置及最短運(yùn)輸路線．（保留畫圖痕跡，并做必要標(biāo)記與注明；不限于尺規(guī)作圖，不要求證明．）
（3）如圖3，若測得AC長為600海里，BD長為500海里，試求出（2）中的最小距離．組卷：763引用：1難度：0.4 -
22．【材料閱讀】在等腰三角形中，我們把底邊與腰長的比叫做頂角的張率（scop）．如圖1，在△XYZ中，XY=XZ，頂角X的張率記作scop∠X=
=底邊腰．容易知道一個(gè)角的大小與這個(gè)角的張率也是相互唯一確定的，所以，類比三角函數(shù)，我們可按上述方式定義∠α（0°＜∠α＜180°） 的張率，例如，scop60°=1，scop90°=YZXY，請根據(jù)材料，完成以下問題：2
如圖2，P是線段AB上的一動(dòng)點(diǎn)（不與點(diǎn)A，B重合），點(diǎn)C，D分別是線段AP，BP的中點(diǎn)，以AC，CD，DB為邊分別在AB的同側(cè)作等邊三角形△ACE，△CDF，△DBG，連接PE和PG．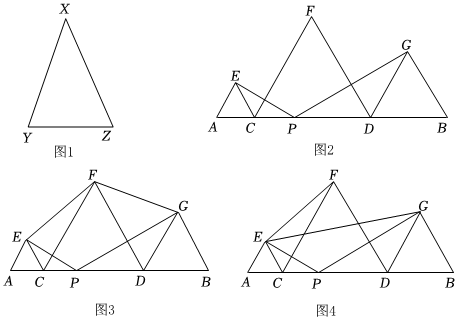
（1）【理解應(yīng)用】
①若等邊三角形△ACE，△CDF，△DBG的邊長分別為a,b,c,則a,b,c三者之間的關(guān)系為 ；
②scop∠EPG=；
（2）【猜想證明】如圖3，連接EF，F(xiàn)G，猜想scop∠EFG的值是多少，并說明理由；
（3）【拓展延伸】如圖4，連接EF，EG，若AB=12，，則△EPG的周長是多少？此時(shí)AP的長為多少？（可直接寫出上述兩個(gè)結(jié)果）EF=27組卷：974引用：2難度：0.1