2022-2023學(xué)年河南省駐馬店市新蔡第一高級中學(xué)高二（上）月考數(shù)學(xué)試卷（理科）（10月份）

一、單選題

• 1．下列直線與直線x-y-1=0平行的是（　　）

  A．x+y-1=0

  B．x-y+1=0

  C．a(chǎn)x-ay-a=0（a≠0）

  D．x-y+1=0或ax-ay-a=0（a≠0）
  組卷：22引用：3難度：0.8

  解析

• 2．“m=-1”是“直線mx+（2m-1）y+1=0和直線3x+my+2=0垂直”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：173引用：16難度：0.9

  解析

• 3．直線x+y=1與圓x²+y²-2ay=0（a＞0）沒有公共點，則a的取值范圍是（　　）

  A．（0， 2 - 1 ）

  B．（ 2 - 1 ， 2 + 1 ）

  C．（ - 2 - 1 ， 2 + 1 ）

  D．（0， 2 + 1 ）
  組卷：4313引用：47難度：0.7

  解析

• 4．若圓x²+y²=1與圓（x-a）²+（y-4）²=16有3條公切線，則正數(shù)a=（　　）

  A．-3

  B．3

  C．5

  D．3或-3
  組卷：490引用：6難度：0.7

  解析

• 5．已知F₁、F₂是橢圓C：

  x

  2

  5

  +

  y

  2

  9

  =

  1

  的焦點，P為C上一點，且|PF₁|=|F₁F₂|，則△PF₁F₂的內(nèi)切圓半徑r=（　　）

  A．1

  B． 5

  C． 15 5

  D． 5 3
  組卷：262引用：11難度：0.7

  解析

• 6．過橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）右焦點F的直線l：x-y-

  3

  =0交C于A，B兩點，P為AB的中點，且OP的斜率為-

  1

  2

  ，則橢圓C的方程為（　　）

  A． x 2 6 + y 2 3 = 1

  B． x 2 7 + y 2 4 = 1

  C． x 2 8 + y 2 5 = 1

  D． x 2 9 + y 2 6 = 1
  組卷：301引用：7難度：0.6

  解析

• 7．已知F₁，F(xiàn)₂是橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的兩個焦點，P為C上一點，且∠F₁PF₂=60°，|PF₁|=5|PF₂|，則C的離心率為（　　）

  A． 21 6

  B． 2 2

  C． 1 2

  D． 2 3
  組卷：1014引用：6難度：0.6

  解析

三、解答題

• 21．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （a＞b＞0）的上頂點E與其左、右焦點F₁、F₂構(gòu)成面積為1的直角三角形．
  （1）求橢圓C的方程；
  （2）過點F₂的直線l交C于A（x₁，y₁），B（x₂，y₂）兩點，P是C上的動點，當(dāng)

  1

  x

  1

  +

  1

  x

  2

  =

  3

  時，求△PAB面積的最大值．
  組卷：87引用：4難度：0.5

  解析

• 22．如圖，橢圓C：

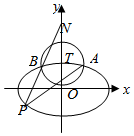  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的離心率為

  3

  2

  ，以橢圓C的上頂點T為圓心作圓T：x²+（y-1）²=r²（r＞0），圓T與橢圓C在第一象限交于點A，在第二象限交于點B．
  （Ⅰ）求橢圓C的方程；
  （Ⅱ）求

  TA

  ?

  TB

  的最小值，并求出此時圓T的方程；
  （Ⅲ）設(shè)點P是橢圓C上異于A，B的一點，且直線PA，PB分別與Y軸交于點M，N，O為坐標(biāo)原點，求證：|OM|?|ON|為定值．
  組卷：710引用：7難度：0.1

  解析