2023-2024學年湖北省云學新高考聯盟學校高二（上）開學聯考數學試卷（8月份）
發布：2024/8/28 4:0:8
一、單選題：本大題共8小題，每個小題5分，共40分.在每小題給出的選項中，只有一項是符合題目要求的.
-
1．容量為8的樣本：3.5，3.8，4.2，4.8，5，5，5.5，6.3，其第75百分數是（ ）
組卷：52引用：5難度：0.7 -
2．在跳水比賽中，有8名評委分別給出某選手原始分，在評定該選手的成績時，從8個原始分中去掉1個最高分和1個最低分，得到6個有效分，這6個有效分與8個原始分相比較，下列說法正確的是（ ）
組卷：278引用：10難度：0.7 -
3．在拋擲硬幣試驗中，記事件A為“正面朝上”，則下列說法正確的（ ）
組卷：125引用：6難度：0.8 -
4．在平行六面體ABCD-A1B1C1D1中，底面ABCD是菱形，側面A1ADD1是正方形，且∠A1AB=120°，∠DAB=60°，AB=2，若P是C1D與CD1的交點，M是A1D1的中點，則MP=（ ）組卷：93引用：5難度：0.5 -
5．已知平面α⊥平面β，直線l?α，則“l⊥β”是“l∥α”的（ ）
組卷：294引用：9難度：0.5 -
6．圓臺O1O2母線長為3，下底直徑為10，上底直徑為5，過圓臺兩條母線作截面，則該截面面積最大值為（ ）
組卷：56引用：3難度：0.8 -
7．二面角α-l-β中，A∈l,C∈l,AB?α，CD?β且AB⊥l,CD⊥l,垂足分別為A、C，AB=2，AC=1，CD=4，已知異面直線AB與CD所成角為60°，則BD=（ ）
組卷：160引用：1難度：0.5
四、解答題：本大題共6小題，共70分.解答應寫出必要的文字說明、證明過程或演算步驟.
-
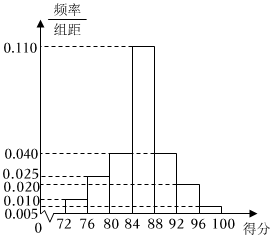21．插花是一種高雅的審美藝術，是表現植物自然美的一種造型藝術，與建筑、盆景等藝術形式相似，是最優美的空間造型藝術之一．為了通過插花藝術激發學生對美的追求，某校舉辦了以“魅力校園、花香溢校園”為主題的校園插花比賽．比賽按照百分制的評分標準進行評分，評委由10名專業教師、10名非專業教師以及20名學生會代表組成，各參賽小組的最后得分為評委所打分數的平均分．比賽結束后，得到甲組插花作品所得分數的頻率分布直方圖和乙組插花作品所得分數的頻數分布表，如下所示：
定義評委對插花作品的“觀賞值”如下所示：分數區間 頻數 [72，76） 1 [76，80） 5 [80，84） 12 [84，88） 14 [88，92） 4 [92，96） 3 [96，100] 1
（1）估計甲組插花作品所得分數的中位數（結果保留兩位小數）；分數區間 [72，84） [84，92） [92，100] 觀賞值 1 2 3
（2）若該校擬從甲、乙兩組插花作品中選出1個用于展覽，從這兩組插花作品的最后得分來看該校會選哪一組，請說明理由（同一組中的數據用該組區間的中點值作代表）；
（3）從40名評委中隨機抽取1人進行調查，試估計其對乙組插花作品的“觀賞值”比對甲組插花作品的“觀賞值”高的概率．組卷：19引用：2難度：0.4 -
22．如圖1，在△ABC中，BC=4，
，AB=13，E，D分別為BC，AC的中點，以DE為折痕，將△DCE折起，使點C到C1的位置，且BC1=2，如圖2．cosB=1313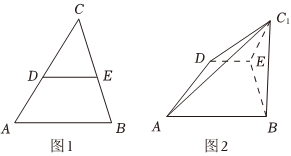
?
（1）設平面C1AD∩平面BEC1=1，證明：l⊥平面ABC1；
（2）P是棱C1D上一點（不含端點）過P、B、E三點作該四棱錐的截面，要求保留畫痕，并說明過程；
（3）若（2）中的截面與面BEC1所成的二面角的正切值為，求該截面將四棱錐分成上下兩部分的體積之比．32組卷：44引用：4難度：0.4