2022-2023學年北京市101中學八年級（下）期中數學試卷

一、選擇題（本題共30分，每小題3分）

• 1．如果

  x

  -

  1

  在實數范圍內有意義，那么x的取值范圍是（　　）

  A．x＞1

  B．x≥l

  C．x≤1

  D．x＜1
  組卷：115引用：4難度：0.8

  解析

• 2．下列各式中，運算正確的是（　　）

  A． 3 3 - 3 = 3

  B． （ - 2 ） 2 = - 2

  C． 2 + 3 = 2 3

  D． 2 × 8 = 4
  組卷：203引用：6難度：0.7

  解析

• 3．在平行四邊形ABCD中，∠D=120°，則∠A的度數等于（　　）

  A．120°

  B．30°

  C．40°

  D．60°
  組卷：80引用：1難度：0.8

  解析

• 4．判斷下列四組數據，可以作為直角三角形三條邊長的是（　　）

  A．0.3，0.4，0.5	B． 3 ， 4 ， 5
  C．3+n,4+n,5+n（n＞0）	D．1，2，3
  組卷：115引用：4難度：0.7

  解析

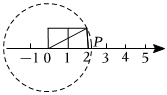• 5．如圖，兩個邊長為1的正方形整齊地排列在數軸上形成一個大的長方形，以O點為圓心，以長方形的對角線長度為半徑作圓與數軸有兩個交點，其中點P表示的數是（　　）

  A． 2

  B． 5

  C．2.2

  D． 3
  組卷：141引用：7難度：0.7

  解析

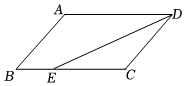• 6．如圖，在平行四邊形ABCD中，DE平分∠ADC，AD=6，BE=2，則平行四邊形ABCD的周長是（　　）

  A．16

  B．18

  C．20

  D．24
  組卷：1234引用：15難度：0.6

  解析

• 7．若直角三角形的兩邊長分別為a、b,且滿足

  a

  2

  -

  6

  a

  +

  9

  +

  |

  b

  -

  4

  |

  =

  0

  ，則該直角三角形的第三邊長為（　　）

  A．5

  B．5或 7

  C．4

  D． 7 或4
  組卷：1247引用：8難度：0.6

  解析

• 8．四邊形ABCD的對角線AC、BD交于點O，下列條件不能判定四邊形ABCD為平行四邊形的是（　　）

  A．∠BAD=∠BCD，∠ABC=∠ADC	B．∠ABC=∠ADC，AB∥CD
  C．AB∥CD，OB=OD	D．AB=CD，OA=OC
  組卷：449引用：6難度：0.6

  解析

• 9．如圖，一只螞蟻從點A出發沿著圓柱體的側面爬行到點B，圓柱體的底面周長是24厘米，圓柱體的高是5厘米，則螞蟻爬行的最短距離為（　　）

  A．13厘米	B．17厘米
  C． （ 5 + 12 π ） 厘米	D．5厘米
  組卷：286引用：2難度：0.6

  解析

三、解答題（本題共52分，第17、18、19、21、22題，每小題4分，第24題3分；第20、23、25題，每小題4分，第26、27題，每小題4分）

• 26．已知平行四邊形ABCD中，AE⊥BC于點E，AE=AD．
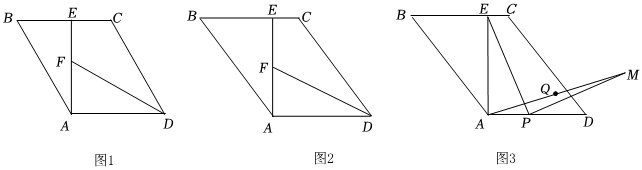
  （1）如圖1，若DF平分∠ADC交線段AE于點F．
  ①當BE=2，∠ADC=60°時，CD=

  ，AF=

  ；
  ②如圖2，若0°＜∠ADC＜90°，且∠ADC≠60°，試探究線段CD，AF，BE之間的數量關系，并證明；
  （2）如圖3，若點P為線段AD上一動點，EP⊥PM，EP=PM．連接AM，點Q是AM中點，且AD=2，當點P從A點運動到D點時，點Q的運動路徑長為

  ．（直接寫出答案）
  組卷：222引用：1難度：0.3

  解析

• 27．已知點E和圖形G，Q為圖形G上一點，若存在點P，使得點E為線段PQ的中點（P，Q不重合），則稱點P為圖形G關于點E的雙倍點．如圖，在平面直角坐標系中，點A（-1，1），B（-2，-1），C（0，-1），D（1，1）．
  （1）若點E的坐標為（-3，0），則在P₁（-4，0），P₂（-5，2），P₃（-6，1），P₄（-7，-1）是四邊形ABCD關于點E的雙倍點的是

  ；
  （2）點N的坐標為（-3，t），若在二四象限角平分線上存在四邊形ABCD關于點N的雙倍點，直接寫出t的取值范圍；
  （3）點M為四邊形ABCD邊上的一個動點，平行于二、四象限角平分線的直線交x軸于點F（a,0），與y軸交于點H（0，b），若線段FH上的所有點均可成為四邊形ABCD關于M的雙倍點，直接寫出b的取值范圍．
  組卷：520引用：2難度：0.1

  解析