2022-2023學年廣西欽州四中九年級（下）期中數學試卷

一、選擇題（本大題共12小題，共60分。在每小題列出的選項中，選出符合題目的一項）

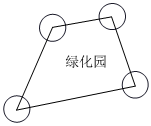• 1．如圖，一塊四邊形綠化園地，四角都做有半徑為2的圓形噴水池，則這四個噴水池占去的綠化園地的面積為（　　）

  A．2π

  B．4π

  C．6π

  D．8π
  組卷：750引用：6難度：0.6

  解析

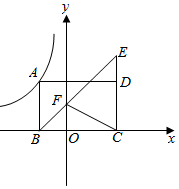• 2．如圖，矩形ABCD中，點A在雙曲線y=-

  8

  x

  上，點B，C在x軸上，延長CD至點E，使CD=2DE，連接BE交y軸于點F，連接CF，則△BFC的面積為（　　）

  A．5

  B．6

  C．7

  D．8
  組卷：5280引用：15難度：0.1

  解析

• 3．下列圖形是中心對稱圖形，也是軸對稱圖形的是（　　）

  A．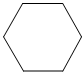

  B．

  C．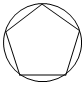

  D．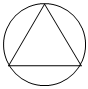
  組卷：57引用：6難度：0.8

  解析

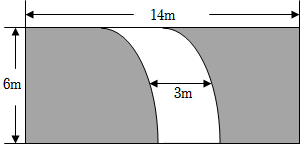• 4．如圖，在一塊長14m、寬6m的長方形場地上，有一條彎曲的道路，其余的部分為綠化區，道路的左邊線向右平移3m就是它的右邊線，則綠化區的面積是（　　）

  A．56m2

  B．66m2

  C．72m2

  D．96m2
  組卷：3390引用：27難度：0.7

  解析

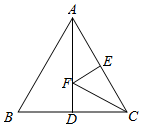• 5．如圖，等邊△ABC的邊長為4，AD是BC邊上的中線，F是AD邊上的動點，E是AC邊上一點，若AE=2，當EF+CF取得最小值時，則∠ECF的度數為（　　）

  A．15°

  B．22.5°

  C．30°

  D．45°
  組卷：3456引用：60難度：0.7

  解析

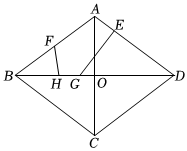• 6．如圖，已知菱形ABCD的對角線AC，BD相交于點O，AC=6，BD=8，點E在AD上，

  AE

  DE

  =

  1

  3

  ，點F為AB的中點，點G，H為BD上的動點，GH=1，連接FH，EG，則FH+EG的最小值為（　　）

  A．4

  B． 17 4

  C． 19 4

  D．5
  組卷：295引用：4難度：0.7

  解析

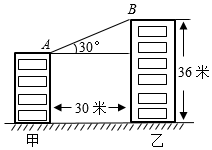• 7．如圖，甲乙兩樓相距30米，乙樓高度為36米，自甲樓頂A 處看乙樓樓頂B處仰角為30°，則甲樓高度為（　　）

  A．11米

  B．（36-15 3 ）米

  C．15 3 米

  D．（36-10 3 ）米
  組卷：2861引用：16難度：0.5

  解析

三、解答題（本大題共5小題，共40分．解答應寫出文字說明，證明過程或演算步驟）

• 20．如圖，AB⊥BC，CD⊥BC，且BC=CD=4cm,AB=1cm,點P以每秒0.5cm的速度從點B開始沿射線BC運動，同時點Q在線段CD上由點C向終點D運動．設運動時間為t秒．
  （1）當t=2時，BP=

  cm,CP=

  cm.
  （2）如圖①，當點P與點Q經過幾秒時，使得△ABP與△PCQ全等？此時，點Q的速度是多少？（寫出求解過程）
  （3）如圖②，是否存在點P，使得△ADP是等腰三角形？若存在，請直接寫出t的值，若不存在，請說明理由．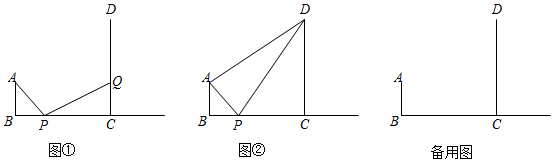
  
  組卷：698引用：10難度：0.2

  解析

• 21．綜合與探究
  如圖1所示，直線y=x+c與x軸交于點A（-4，0），與y軸交于點C，拋物線y=-x²+bx+c經過點A，C．
  （1）求拋物線的解析式
  （2）點E在拋物線的對稱軸上，求CE+OE的最小值；
  （3）如圖2所示，M是線段OA的上一個動點，過點M垂直于x軸的直線與直線AC和拋物線分別交于點P、N．
  ①若以C，P，N為頂點的三角形與△APM相似，則△CPN的面積為

  ；
  ②若點P恰好是線段MN的中點，點F是直線AC上一個動點，在坐標平面內是否存在點D，使以點D，F，P，M為頂點的四邊形是菱形？若存在，請直接寫出點D的坐標；若不存在，請說明理由．
  注：二次函數y=ax²+bx+c（a≠0）的頂點坐標為（-

  b

  2

  a

  ，

  4

  ac

  -

  b

  2

  4

  a

  ）
  
  組卷：2332引用：5難度：0.1

  解析