2022-2023學年重慶外國語學校高一（上）期中數學試卷

一、單項選擇題（共8個小題，每小題5分，共40分.每小周的四個地項中，只有一個符合題目要求）

• 1．若集合P={x|x²+x-2≤0}，Q={x∈Z|-2＜x＜4}，則P∩Q=（　　）

  A．{-1，0，1}

  B．{-1，0}

  C．{0，1}

  D．{0，1，2}
  組卷：36引用：1難度：0.8

  解析

• 2．設a∈R，則“|a|≥10”是“a²≥9”的（　　）

  A．充要條件	B．充分不必要條件
  C．必要不充分條件	D．既不必要也不充分條件
  組卷：24引用：1難度：0.7

  解析

• 3．函數

  y

  =

  x

  2

  +

  2

  x

  -

  8

  的單調遞增區間是（　　）

  A．[-1，+∞）

  B．[1，+∞）

  C．[2，+∞）

  D．[4，+∞）
  組卷：112引用：1難度：0.7

  解析

• 4．小明騎車上學，開始時勻速行駛，途中因交通堵塞停留了一段時間，后為了趕時間加快速度行駛．與以上事件吻合得最好的圖象是（　　）

  A．	B．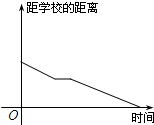
  C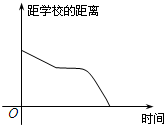．	D．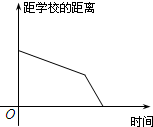
  組卷：2273引用：62難度：0.9

  解析

• 5．已知不等式ax²+bx-a³＜0的解集是{x|x＞9或x＜-1），則a+b的值為（　　）

  A．-27

  B．-21

  C．27

  D．21
  組卷：50引用：1難度：0.7

  解析

• 6．設函數f（x）=x-

  2

  x

  +1在[1，4]上的值域為（　　）

  A． [ 1 ， 9 2 ]

  B．[0，1]

  C． [ 0 ， 9 2 ]

  D． [ 2 ， 9 2 ]
  組卷：212引用：3難度：0.7

  解析

• 7．設正實數x,y滿足

  3

  x

  +

  y

  2

  =

  2

  ，則

  4

  2

  x

  +

  1

  +

  6

  y

  +

  1

  的最小值為（　　）

  A． 9 + 6 2 4

  B． 3 2

  C． 7 + 4 2 4

  D． 4 2
  組卷：116引用：2難度：0.7

  解析

四、解答題（共6小題，共70分.解答應寫出文字說明，證明過程郵城演算步驟.）

• 21．已知定義在（0，+∞）上的函數f（x）滿足：①對任意的x,y∈（0，+∞），都有f（xy）=f（x）+f（y）；②當且僅當x＞1時，f（x）＜0成立．
  （1）求f（1）；
  （2）類比以下比較f（2）與f（3）的大小關系，嘗試判斷f（x）的單調性，并用定義證明；

  f

  （

  3

  ）

  -

  f

  （

  2

  ）

  =

  f

  （

  3

  2

  ×

  2

  ）

  -

  f

  （

  2

  ）

  =

  f

  （

  3

  2

  ）

  +

  f

  （

  2

  ）

  -

  f

  （

  2

  ）

  =

  f

  （

  3

  2

  ）

  ＜

  0

  ，所以f（3）＜f（2）．
  （3）若存在x∈（0，+∞），使得不等式

  f

  （

  x

  2

  +

  1

  x

  2

  ）

  ≥

  f

  [

  m

  （

  x

  +

  1

  x

  ）

  -

  4

  ]

  成立，求實數m的取值范圍．
  組卷：57引用：1難度：0.5

  解析

• 22．設函數的定義域為D，如果存在[a,b]∈D，使得f（x）在[a,b]上的值域也為[a,b]，則稱f（x）為“A佳”函數．已知冪函數

  f

  （

  x

  ）

  =

  （

  p

  2

  +

  p

  -

  1

  ）

  x

  p

  -

  1

  2

  在（0，+∞）內是單調增函數．
  （1）求函數f（x）的解析式：
  （2）

  g

  （

  x

  ）

  =

  f

  （

  x

  ）

  -

  2

  9

  是否為“A佳”函數．若是，請指出所在區間；若不是，請說明理由．
  （3）若函數h（x）=n-f（x+1），且h（x）是“A佳”函數，試求出實數n的取值范圍．
  組卷：22引用：2難度：0.6

  解析