2021-2022學(xué)年廣東省深圳市第二高級中學(xué)高一（上）入學(xué)數(shù)學(xué)試卷

一．選擇題（本大題共10個小題，每題4分，共40分；在每個小題給出的四個選項中只有一個選項是正確的）

• 1．對于任何有理數(shù)a,下列各式中一定為負(fù)數(shù)的是（　　）

  A．-（-3+a）

  B．-a

  C．-|a+1|

  D．-|a|-1
  組卷：15引用：1難度：0.8

  解析

• 2．若實數(shù)m、n滿足等式|m-2|+

  n

  -

  4

  =0，且m、n恰好是等腰△ABC的兩條邊的邊長，則△ABC的周長是（　　）

  A．6

  B．8

  C．10

  D．8或10
  組卷：17引用：1難度：0.9

  解析

• 3．如圖，一次函數(shù)y=kx+b（k＞0）的圖象過點（-1，0），則不等式k（x-1）+b＞0的解集是（　　）

  A．{x|x＞-2}

  B．{x|x＞-1}

  C．{x|x＞0}

  D．{x|x＞1}
  組卷：69引用：1難度：0.9

  解析

• 4．如圖，函數(shù)y=ax²-2x+1和y=ax-a（a是常數(shù)，且a≠0）在同一平面直角坐標(biāo)系的圖象可能是（　　）

  A．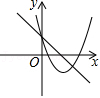

  B．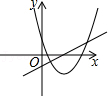

  C．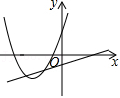

  D．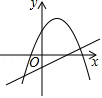
  組卷：41引用：1難度：0.8

  解析

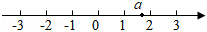• 5．實數(shù)a在數(shù)軸上的對應(yīng)點的位置如圖所示．若實數(shù)b滿足-a＜b＜a,則b的值可以是（　　）

  A．2

  B．-1

  C．-2

  D．-3
  組卷：21引用：1難度：0.9

  解析

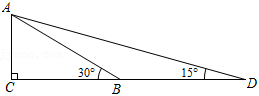• 6．構(gòu)建幾何圖形解決代數(shù)問題是“數(shù)形結(jié)合”思想的重要應(yīng)用，在計算tan15°時，如圖．在Rt△ACB中，∠C=90°，∠ABC=30°，延長CB使BD=AB，連接AD，得∠D=15°，所以tan15°=

  AC

  CD

  =

  1

  2

  +

  3

  =

  2

  -

  3

  （

  2

  +

  3

  ）

  （

  2

  -

  3

  ）

  =2-

  3

  ．類比這種方法，計算tan22.5°的值為（　　）

  A． 2 +1

  B． 2 -1

  C． 2

  D． 1 2
  組卷：68引用：1難度：0.6

  解析

• 7．若a≠b,且a²-4a+1=0，b²-4b+1=0，則

  1

  1

  +

  a

  2

  +

  1

  1

  +

  b

  2

  的值為（　　）

  A． 1 4

  B．1

  C．4

  D．3
  組卷：66引用：1難度：0.7

  解析

三．解答題（16題6分，17題6分，18～21題每題12分）

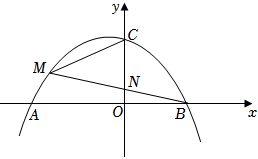• 20．如圖，拋物線y=ax²+ax-12a（a＜0）與x軸交于A、B兩點（A在B的左側(cè)），與y軸交于點C，點M是第二象限內(nèi)拋物線上一點，BM交y軸于N．
  （1）求點A、B的坐標(biāo)；
  （2）若BN=MN，且S_△MBC=

  27

  4

  ，求a的值；
  （3）若∠BMC=2∠ABM，求

  MN

  NB

  的值．
  組卷：63引用：1難度：0.3

  解析

• 21．某數(shù)學(xué)課外活動小組在學(xué)習(xí)了勾股定理之后，針對圖1中所示的“由直角三角形三邊向外側(cè)作多邊形，它們的面積S₁，S₂，S₃之間的關(guān)系問題”進(jìn)行了以下探究：
  類比探究
  （1）如圖2，在Rt△ABC中，BC為斜邊，分別以AB，AC，BC為斜邊向外側(cè)作Rt△ABD，Rt△ACE，Rt△BCF，若∠1=∠2=∠3，則面積S₁，S₂，S₃之間的關(guān)系式為______；
  推廣驗證
  （2）如圖3，在Rt△ABC中，BC為斜邊，分別以AB，AC，BC為邊向外側(cè)作任意△ABD，△ACE，△BCF，滿足∠1=∠2=∠3，∠D=∠E=∠F，則（1）中所得關(guān)系式是否仍然成立？若成立，請證明你的結(jié)論；若不成立，請說明理由；
  拓展應(yīng)用
  （3）如圖4，在五邊形ABCDE中，∠A=∠E=∠C=105°，∠ABC=90°，AB=2

  3

  ，DE=2，點P在AE上，∠ABP=30°，PE=

  2

  ，求五邊形ABCDE的面積．
  
  組卷：39引用：1難度：0.5

  解析