2022-2023學年廣東省梅州市五華縣大都中學七年級（下）開學數學試卷
發布：2024/4/20 14:35:0
一、單選題。本大題共10小題，每小題3分，共30分。
-
1．用?表示實心圓，用〇表示空心圓，現有若干實心圓和空心圓按下列規律排列，?〇??〇???〇?〇??〇???〇?〇??〇???〇?，則前2008個圓中的實心圓有（ ）
組卷：43引用：3難度：0.7 -
2．如圖所示，數軸上點A、B對應的有理數分別為a、b,下列說法正確的是（ ）組卷：1153引用：23難度：0.7 -
3．已知一列數，a1=
，a2=22-a0，a3=22-a1，a4=22-a2…，當a0=3時，則a2018等于（ ）22-a3組卷：783引用：3難度：0.5 -
4．一款新型的太陽能熱水器進價2000元，標價3000元，若商場要求以利潤率不低于5%的售價打折出售，則設銷售員出售此商品最低可打x折，由題意列方程，得（ ）
組卷：1463引用：10難度：0.9 -
5．若a、b互為相反數，c和d互為倒數，m是最大的負整數，則a+b-cd+m2017的值是（ ）
組卷：146引用：6難度：0.6 -
6．設M=x2+8x+12，N=-x2+8x-3，那么M與N的大小關系是（ ）
組卷：1344引用：3難度：0.5 -
7．已知2＜a＜4，則化簡
+1-2a+a2的結果是（ ）a2-8a+16組卷：1440引用：4難度：0.7 -
8．已知代數式（a2+a+2b）-（a2+3a+mb）的值與b的值無關，則m的值為（ ）
組卷：236引用：6難度：0.7
三、解答題：第18，19，20小題6分，第21，22，23小題9分，第24，25小題10分。
-
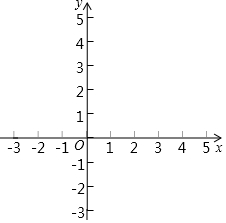24．對于平面直角坐標系xOy中的任意兩點M（x1，y1），N（x2，y2），給出如下定義：
將|x1-x2|稱為點M，N之間的“橫長”，|y1-y2|稱為點M，N之間的縱長”，點M與點N的“橫長”與“縱長”之和稱為“折線距離”，記作d（M，N）=|x1-x2|+|y1-y2|．
例如：若點M（-1，1），點N（2，-2），則點M與點N的“折線距離”為：d（M，N）=|-1-2|+|1-（-2）|=3+3=6．
根據以上定義，解決下列問題：
已知點P（3，2），
（1）若點A（a,2），且d（P，A）=5，求a的值；
（2）已知點B（b,b），且d（P，B）＜3，直接寫出b的取值范圍；
（3）若第一象限內的點T與點P的“橫長”與“縱長”相等，且d（P，T）＞5，簡要分析點T的橫坐標t的取值范圍．組卷：618引用：4難度：0.6 -
25．定義：對任意一個兩位數a,如果a滿足個位數字與十位數字互不相同，且都不為零，那么稱這個兩位數為“迥異數”．將一個“迥異數”的個位數字與十位數字對調后得到一個新的兩位數，把這個新兩位數與原兩位數的和與11的商記為f（a）．
例如：a=12，對調個位數字與十位數字得到新兩位數21，新兩位數與原兩位數的和為21+12=33，和與11的商為33÷11=3，所以f（12）=3．
根據以上定義，回答下列問題：
（1）填空：下列兩位數：40，51，66中，“迥異數”為 ；
（2）計算：
①f（13）；
②f（10a+b）；
（3）如果一個“迥異數”m的十位數字是x,個位數字是x-4，另一個“迥異數”n的十位數字是x-5，個位數字是2，且滿足f（m）-f（n）＜8，求x.組卷：117引用：2難度：0.6