2017-2018學(xué)年北京四中九年級(jí)（下）開(kāi)學(xué)數(shù)學(xué)試卷

一、選擇題．

• 1．已知一粒米的質(zhì)量是0.000021千克，這個(gè)數(shù)字用科學(xué)記數(shù)法表示為（　　）

  A．21×10-4千克	B．2.1×10-6千克
  C．2.1×10-5千克	D．2.1×10-4千克
  組卷：312引用：34難度：0.9

  解析

• 2．若代數(shù)式

  x

  x

  -

  4

  有意義，則實(shí)數(shù)x的取值范圍是（　　）

  A．x=0

  B．x=4

  C．x≠0

  D．x≠4
  組卷：3431引用：30難度：0.9

  解析

• 3．在一個(gè)不透明的口袋中裝有5個(gè)完全相同的小球，把它們分別標(biāo)號(hào)為1，2，3，4，5，從中隨機(jī)摸出一個(gè)小球，其標(biāo)號(hào)大于2的概率為（　　）

  A． 1 5

  B． 2 5

  C． 3 5

  D． 4 5
  組卷：526引用：92難度：0.9

  解析

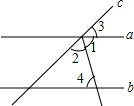• 4．如圖，直線a,b被直線c所截，a∥b,∠1=∠2，若∠3=40°，則∠4等于（　　）

  A．40°

  B．50°

  C．70°

  D．80°
  組卷：2716引用：102難度：0.9

  解析

• 5．下面的幾何體中，主視圖為三角形的是（　　）

  A．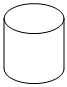

  B．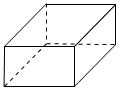

  C．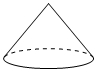

  D．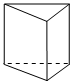
  組卷：139引用：118難度：0.9

  解析

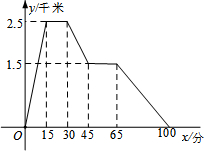• 6．如圖圖象所反映的過(guò)程是：明明從家跑步去體育場(chǎng)，在那里鍛煉了一陣后，又去早餐店吃早餐，然后散步走回家．其中x表示時(shí)間（分），y（千米）表示明明離家的距離．根據(jù)圖象提供的信息，以下四個(gè)說(shuō)法錯(cuò)誤的是（　　）

  A．明明家離體育場(chǎng)2.5千米

  B．明明在體育場(chǎng)鍛煉了15分鐘

  C．體育場(chǎng)離早餐店1千米

  D．明明從早餐店回家的平均速度是3千米/小時(shí)
  組卷：75引用：2難度：0.7

  解析

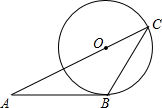• 7．如圖，AB與⊙O相切于點(diǎn)B，AO的延長(zhǎng)線交⊙O于點(diǎn)C，連接BC，若∠ABC=120°，OC=3，則

  ?

  BC

  的長(zhǎng)為（　　）

  A．π

  B．2π

  C．3π

  D．5π
  組卷：382引用：19難度：0.9

  解析

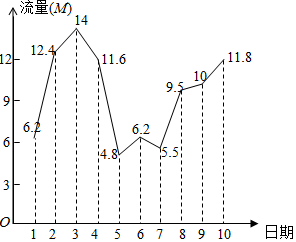• 8．小王的手機(jī)使用的是每月300M流量套餐，圖中記錄了小王在4月1日至4月10日這十天的流量使用情況，下列敘述中正確的是（　　）

  A．1日-10日這10天的平均流量小于9.0M/日

  B．11日-30日這20天，如果每天的平均流量不超過(guò)11M，這個(gè)月總流量就不會(huì)超過(guò)套餐流量

  C．從1日-10這10天的流量中任選連續(xù)3天的流量，則3日，4日，5日這三天的流量的方差最大

  D．從1-10日這10天中的流量中任選連續(xù)3天的流量，則8日，9日，10日這三天的流量的方差最小
  組卷：17引用：1難度：0.7

  解析

二、填空題．

• 9．分解因式：mn²+6mn+9m=

  ．
  組卷：433引用：39難度：0.9

  解析

三、解答題．

• 27．在正方形ABCD中，點(diǎn)P是邊BC上一動(dòng)點(diǎn)（不包含端點(diǎn)），線段AP的垂直平分線與AB、AP、BD、CD分別交于點(diǎn)M、E、F、N．
  （1）如圖1，若PB=a,AB=3a,求線段MN的長(zhǎng)度；
  （2）用等式表示ME、EF、NF之間的數(shù)量關(guān)系并證明．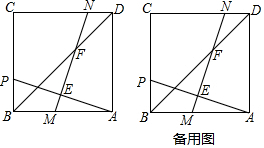
  
  組卷：756引用：1難度：0.3

  解析

• 28．對(duì)于半徑為r的⊙P及一個(gè)正方形給出如下定義：若⊙P上存在到此正方形四條邊距離都相等的點(diǎn)，則稱⊙P是該正方形的“等距圓”．如圖1，在平面直角坐標(biāo)系xOy中，正方形ABCD的頂點(diǎn)A的坐標(biāo)為（2，4），頂點(diǎn)C、D在x軸上，且點(diǎn)C在點(diǎn)D的左側(cè)．
  （1）當(dāng)r=3

  2

  時(shí)，
  ①在P₁（

  2

  ，6），P₂（-4，0），P₃（1，1）中可以成為正方形ABCD的“等距圓”的圓心的是

  ．
  ②若點(diǎn)P在直線y=x+2上，且⊙P是正方形ABCD的“等距圓”，則點(diǎn)P的坐標(biāo)為

  ．
  （2）如圖2，在正方形ABCD所在平面直角坐標(biāo)系xOy中，正方形EFGH的頂點(diǎn)F的坐標(biāo)為（6，2），頂點(diǎn)E、H在y軸上，且點(diǎn)H在點(diǎn)E的上方．
  ①若⊙P同時(shí)為上述兩個(gè)正方形的“等距圓”，且與BC所在直線相切，求⊙P的半徑；
  ②正方形ABCD繞著點(diǎn)O旋轉(zhuǎn)一周，在旋轉(zhuǎn)的過(guò)程中，線段HF上沒(méi)有一個(gè)點(diǎn)能成為它的“等距圓”的圓心，則正方形ABCD的等距圓的半徑r的取值范圍是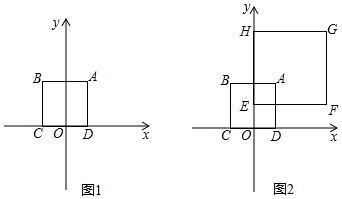

  ．
  
  組卷：183引用：1難度：0.2

  解析