2023年廣東省東莞中學松山湖學校中考數學一模試卷

一、選擇題：本題共10小題，每小題3分，共30分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．|-2023|=（　　）

  A．2023

  B．-2023

  C．- 1 2023

  D． 1 2023
  組卷：590引用：21難度：0.7

  解析

• 2．在下列圖形中，是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：52引用：4難度：0.9

  解析

• 3．神舟十三號飛船在近地點高度200000m,遠地點高度356000m的軌道上駐留了6個月后，于2022年4月16日順利返回．將數字356000用科學記數法表示為（　　）

  A．3.56×105

  B．0.356×106

  C．3.56×106

  D．35.6×104
  組卷：1326引用：31難度：0.9

  解析

• 4．已知點（-1，y₁），（3，y₂）在一次函數y=2x+1的圖象上，則y₁，y₂的大小關系是（　　）

  A．y1＜y2

  B．y1=y2

  C．y1＞y2

  D．不能確定
  組卷：2046引用：13難度：0.8

  解析

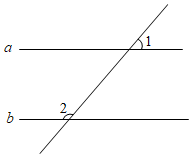• 5．如圖，直線a∥b,∠1=50°，∠2的度數為（　　）

  A．100°

  B．120°

  C．130°

  D．150°
  組卷：349引用：3難度：0.8

  解析

• 6．數據2、3、3、5、4的中位數是（　　）

  A．2

  B．3

  C．3.5

  D．4
  組卷：112引用：3難度：0.8

  解析

• 7．下列運算正確的是（　　）

  A．3a-2a=1	B．a3?a5=a8
  C．a8÷2a2=2a4	D．（3ab）2=6a2b2
  組卷：369引用：8難度：0.7

  解析

五、解答題（三）：本大題2小題，每小題12分，共24分．

• 22．（1）已知正方形ABCD，E為對角線AC上一動點，將BE繞點B順時針旋轉90°到BF處，得△BEF，連接CF，如圖1，填空：
  ①

  CF

  AE

  =

  ；
  ②∠ACF的度數為

  ．
  （2）在矩形ABCD和Rt△BEF中，∠EBF=90°，∠ACB=∠EFB=60°，連接CF，如圖2，請判斷

  CF

  AE

  的值及∠ACF的度數，并說明理由．
  （3）在（2）的條件下，取EF的中點M，連接BM、CM，若AB=2

  3

  ，則當△CBM是直角三角形時，請直接寫出線段CF的長．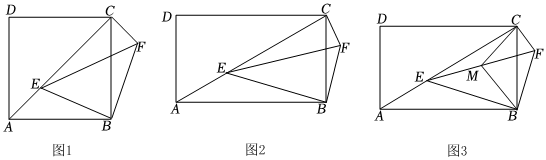
  
  組卷：327引用：3難度：0.4

  解析

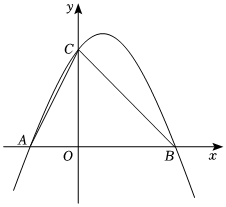• 23．如圖，在平面直角坐標系中，已知拋物線經過點A（-1，0）和點B（3，0），點C為y軸正半軸一點，CO=BO．
  （1）求這條拋物線所對應的函數表達式；
  （2）點P為該拋物線在第一象限上的點（不與點B、C重合），求△CPB面積的最大值及此時點P的坐標：
  （3）點M是y軸上的動點，當∠OCA=∠OCB-∠OMA時，求M的坐標．
  組卷：520引用：2難度：0.4

  解析