2023-2024學年福建省泉州六中八年級（上）第一次月考數學試卷

一、選擇題（本大題共10小題，共40.0分。在每小題列出的選項中，選出符合題目的一項）

• 1．64的立方根是（　　）

  A．±8

  B．±4

  C．8

  D．4
  組卷：808引用：180難度：0.9

  解析

• 2．下列各式中，正確的是（　　）

  A． 25 =± 5

  B． ± 25 =5

  C． （ - 5 ） 2 =-5

  D． 3 - 125 = - 5
  組卷：782引用：15難度：0.9

  解析

• 3．下列四個數：-3，-

  3

  ，-π，-1，其中最小的數是（　　）

  A．-π

  B．-3

  C．-1

  D．- 3
  組卷：1696引用：27難度：0.9

  解析

• 4．在-

  5

  ，3.14，0，

  3

  8

  ，

  22

  7

  ，-

  π

  2

  ，0.1010010001…（相鄰兩個1之間0的個…數逐次加）．這7個數中，無理數共有（　　）

  A．2個

  B．3個

  C．4個

  D．5個
  組卷：177引用：5難度：0.7

  解析

• 5．下列運算正確的是（　　）

  A．a4+a2=a6	B．（-2a2）3=-6a8
  C．6a-a=5	D．a2?a3=a5
  組卷：221引用：5難度：0.9

  解析

• 6．已知3m-1和-2m-2是某正數a的平方根，則a的值是（　　）

  A．3

  B．64

  C．3或- 1 5

  D．64或 64 25
  組卷：1556引用：7難度：0.6

  解析

• 7．已知a,b,c為自然數，且滿足2^a×3^b×4^c=192，則a+b+c的取值不可能是（　　）

  A．5

  B．6

  C．7

  D．8
  組卷：6185引用：23難度：0.8

  解析

• 8．若（x²+p）（x²-qx+4）的乘積中不含x²與x³項，則p+q的值為（　　）

  A．-4

  B．-8

  C．-2

  D．8
  組卷：932引用：4難度：0.7

  解析

三、解答題（本大題共9小題，共86.0分。解答應寫出文字說明，證明過程或演算步驟）

• 24．數形結合是一種重要的數學思想方法，利用圖1中邊長分別為a、b的兩個正方形紙片和長為b、寬為a的長方形紙片，可以拼出一些圖形來解釋某些等式，如，由圖2可得（a+2b）（a+b）=a²+3ab+b².則：
  （1）由圖3可以解釋的等式是

  ；
  （2）用9張邊長為a的正方形紙片，12張長為b、寬為a的長方形紙片，4張邊長為b的正方形紙片拼成一個大正方形，求這個大正方形的邊長；
  （3）用5張長為b寬為a的長方形紙片按照圖4方式不重疊地放在大長方形ABCD內，大長方形中未被覆蓋的兩個部分的面積設為S₁、S₂，BC的長設為x.
  ①請用含x的代數式表示：2S₂-3S₁；
  ②若無論x取任何實數時，①的結果始終保持不變，請直接寫出a與b滿足的數量關系．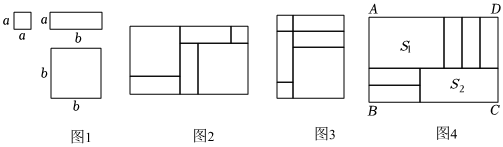
  
  組卷：345引用：4難度：0.5

  解析

• 25．【初步探索】
  （1）如圖1：在四邊形ABCD中，AB=AD，∠B=∠ADC=90°，E、F分別是BC、CD上的點，且EF=BE+FD，探究圖中∠BAE、∠FAD、∠EAF之間的數量關系．
  小王同學探究此問題的方法是：延長FD到點G，使DG=BE．連接AG，先證明△ABE≌△ADG，再證明△AEF≌△AGF，可得出結論，他的結論應是

  ；
  【靈活運用】
  （2）如圖2，若在四邊形ABCD中，AB=AD，∠B+∠D=180°．E、F分別是BC、CD上的點，且EF=BE+FD，上述結論是否仍然成立，并說明理由；
  【拓展延伸】
  （3）如圖3，已知在四邊形ABCD中，∠ABC+∠ADC=180°，AB=AD，若點E在CB的延長線上，點F在CD的延長線上，如圖3所示，仍然滿足EF=BE+FD，請寫出∠EAF與∠DAB的數量關系，并給出證明過程．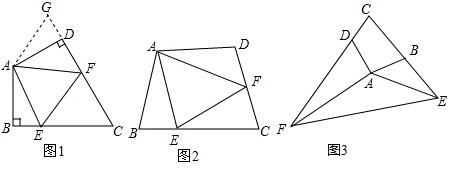
  
  組卷：4488引用：52難度：0.1

  解析