當前位置：試卷中心 > 試卷詳情

2021-2022學年江蘇省鹽城市亭湖區景山中學八年級（下）期中數學試卷

發布：2025/1/2 10:30:4

一、選擇題：（每題3分，共24分）

1．下列防控疫情的圖標中，既是軸對稱圖形，又是中心對稱圖形的是（　　）
A． B． C． D．
組卷：536引用：30難度：0.8
解析
2．下列調查適合用普查的是（　　）
A．長江中現有魚的種類
B．某品牌燈泡的使用壽命
C．全校學生最喜愛的體育項目
D．一批食品中防腐劑的含量
組卷：81引用：4難度：0.7
解析
3．在以下式子中，x可以取到3和4的是（　　）
A．
2
x
-
3
B．
2
x
-
4
C．
x
-
3
D．
x
-
4
組卷：120引用：3難度：0.9
解析
4．菱形具有而矩形不一定具有的性質是（　　）
A．內角和等于360度 B．對角相等
C．對邊平行且相等 D．對角線互相垂直
組卷：86引用：4難度：0.5
解析
5．若關于x的一元二次方程kx²-2x-1=0有實數根，則k的取值范圍是（　　）
A．k≥-1且k≠0 B．k≥-1 C．k≤1 D．k≤1且k≠0
組卷：501引用：22難度：0.9
解析
6．一次函數y=kx-k與反比例函數y=
k
x
在同一平面直角坐標系內的圖象大致為（　　）
A． B． C． D．
組卷：133引用：3難度：0.7
解析
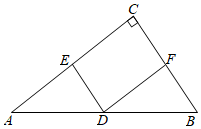7．如圖，在Rt△ABC中，點D，E，F分別是邊AB，AC，BC的中點，AC=8，BC=6，則四邊形CEDF的面積是（　　）
A．6 B．12 C．24 D．48
組卷：673引用：8難度：0.4
解析
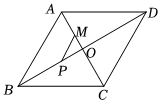8．如圖，在菱形ABCD中，AB=AC=10，對角線AC、BD相交于點O，點M在線段AC上，且AM=4，點P為線段BD上的一個動點，則MP+
1
2
PB的最小值是（　　）
A．4 B．
3
2
C．
3
3
D．5
組卷：472引用：3難度：0.4
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題：（共72分）

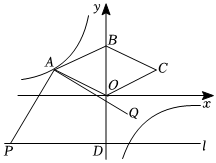25．如圖，菱形OABC的點B在y軸上，點C坐標為（8，6），雙曲線
y
=
k
x
的圖象經過點A．
（1）菱形OABC的邊長為
；
（2）求雙曲線的函數關系式；
（3）點B關于點O的對稱點為D點，過D作直線l垂直于x軸，點P是直線l上一個動點，
①將點P繞點A逆時針旋轉90°得點Q，當點Q落在雙曲線上時，求點Q的坐標．
②點E在雙曲線上，當P、E、A、B四點構成平行四邊形時，求點E的坐標．
組卷：157引用：1難度：0.1
解析
26．某校數學課外活動小組的同學，針對兩個正數之和與這兩個正數之積的算術平方根的兩倍之間的關系進行了探究，請閱讀以下探究過程并解決問題．
【探究發現】
6+6=2
6
×
6
=12；
1
5
+
1
5
=
2
1
5
×
1
5
=
2
5
；
0.3+0.3=2
0
.
3
×
0
.
3
=0.6；
1
3
+
3
＞
2
1
3
×
3
=2；
0.2+3.2＞2
0
.
2
×
3
.
2
=1.6；
1
3
+
1
27
＞
2
1
3
×
1
27
=
2
9
．
【猜想結論】
如果a＞0，b＞0，那么存在a+b≥2
ab
（當且僅當a=b時，等號成立）．
【證明結論】
∵
（
a
-
b
）
2
≥0，
∴①當且僅當
a
-
b
=0，即a=b時，a-2
ab
+b=0，∴a+b=2
ab
；
②當
a
-
b
≠0，即a≠b時，a-2
ab
+b＞0，∴a+b＞2
ab
．
綜合上述可得：若a＞0，b＞0，則a+b≥2
ab
成立（當且僅當a=b時，等號成立）．
（1）【應用結論】已知函數y₁=x（x＞0）與函數y₂=
1
x
（x＞0），則當x=時，y₁+y₂取得最小值為．
（2）【應用結論】對于函數y=
1
x
-
4
+x（x＞4），當x取何值時，函數y的值最小？最小值是多少？
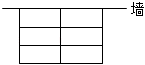
（3）【拓展應用】疫情期間，高速公路某檢測站入口處，為了解決疑似人員的臨時隔離問題，檢測人員利用檢測站的一面墻（墻的長度不限），計劃用鋼絲網圍成6間相同的長方形隔離房．如圖，已知每間隔離房的面積24m²，問：每間隔離房的長、寬各為多少米時，所用鋼絲網長度最短？最短長度是多少？
組卷：251引用：2難度：0.1
解析