2023年黑龍江省哈爾濱三中高考數學二模試卷

一、單項選擇題（共8小題，每小題5分，在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．若集合

  A

  =

  {

  x

  |

  y

  =

  1

  -

  x

  }

  ，B={x|x²-2x≥0}，則A∩B=（　　）

  A．（-∞，0]

  B．（0，1]

  C．（-∞，0）

  D．[0，1]
  組卷：100引用：3難度：0.7

  解析

• 2．若復數

  z

  =

  2

  +

  i

  1

  -

  i

  ，則|z|=（　　）

  A．1

  B． 10 2

  C． 10 4

  D． 10
  組卷：208引用：12難度：0.7

  解析

• 3．已知

  |

  b

  |

  =

  3

  ，且

  a

  ?

  b

  =

  -

  2

  ，則向量

  a

  在向量

  b

  上的投影向量為（　　）

  A． - 2 3 a

  B． 2 3 a

  C． - 2 3 b

  D． 2 3 b
  組卷：457引用：3難度：0.6

  解析

• 4．已知命題p：tanα=3，命題q：cos2α=-

  4

  5

  ，則命題p是命題q的（　　）

  A．充要條件	B．充分不必要條件
  C．必要不充分條件	D．既不充分也不必要條件
  組卷：98引用：1難度：0.7

  解析

• 5．在

  （

  3

  x

  -

  2

  x

  ）

  8

  的展開式中，常數項為（　　）

  A．-112

  B．112

  C．-1120

  D．1120
  組卷：475引用：2難度：0.8

  解析

• 6．圭表，是度量日影長度的一種天文儀器，由“圭”和“表”兩個部件組成．圭表和日晷一樣，也是利用日影進行測量的古代天文儀器．所謂高表測影法，通俗的說，就是垂直于地面立一根桿，通過觀察記錄它正午時影子的長短變化來確定季節的變化．垂直于地面的直桿叫“表”，水平放置于地面上刻有刻度以測量影長的標尺叫“圭”，如圖1，利用正午時太陽照在表上，表在圭上的影長來確定節令．已知某地夏至和冬至正午時，太陽光線與地面所成角分別約為α，β，如圖2，若影長之差CD=a尺，則表高AB為（　　）尺．
  

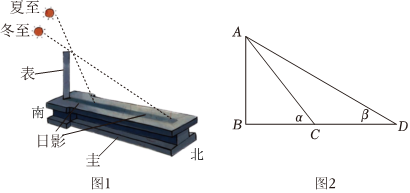
  A． a （ tanα - tanβ ） tanαtanβ	B． tanα - tanβ atanαtanβ
  C． atanαtanβ tanα - tanβ	D． tanαtanβ a （ tanαtanβ ）
  組卷：180引用：1難度：0.5

  解析

• 7．設f（x）是定義在R上的可導函數，f（x）的導函數為f'（x），且f'（x）?f（x）＞2x³在R上恒成立，則下列說法中正確的是（　　）

  A．f（2023）＜f（-2023）	B．f（2023）＞f（-2023）
  C．|f（2023）|＜|f（-2023）|	D．|f（2023）|＞|f（-2023）|
  組卷：128引用：2難度：0.4

  解析

三、解答題：（共70分，解答應寫出文字說明、證明過程或演算步驟）

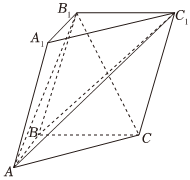• 21．如圖，三棱柱ABC-A₁B₁C₁中，AA₁⊥A₁B₁，AB⊥BC，側面BCC₁B₁為菱形．
  （1）求證：平面ABC₁⊥平面AB₁C；
  （2）若BC=2AB=2，∠B₁BC=60°，求二面角B₁-AC₁-B的正弦值．
  組卷：106引用：1難度：0.5

  解析

• 22．我國南北朝時期的數學家祖沖之（公元429年-500年）計算出圓周率的精確度記錄在世界保持了千年之久，德國數學家魯道夫（公元1540年-1610年）用一生精力計算出了圓周率的35位小數，隨著科技的進步，一些常數的精確度不斷被刷新．例如：我們很容易能利用計算器得出函數J（x）=e^x+x（e=2.71828…）的零點x₀的近似值，為了實際應用，本題中取x₀的值為-0.57．哈三中畢業生創辦的倉儲型物流公司建造了占地面積足夠大的倉庫，內部建造了一條智能運貨總干線C₁，其在已經建立的直角坐標系中的函數解析式為

  g

  （

  x

  ）

  =

  ln

  （

  x

  -

  2

  -

  1

  x

  0

  ）

  ，其在x=2處的切線為L₁：y=ψ（x）．現計劃再建一條總干線C₂：y=e^x+m，其中m為待定的常數．
  注明：本題中計算的最終結果均用數字表示．
  （1）求出L₁的直線方程，并且證明：在直角坐標系中，智能運貨總干線C₁上的點不在直線L₁的上方；
  （2）在直角坐標系中，設直線

  L

  2

  ：

  y

  =

  ψ

  （

  x

  -

  x

  0

  3

  ）

  ，計劃將倉庫中直線L₁與L₂之間的部分設為隔離區，兩條運貨總干線C₁、C₂分別在各自的區域內，即曲線C₂上的點不能越過直線L₂，求實數m的取值范圍．
  組卷：58引用：4難度：0.3

  解析