當前位置：試卷中心 > 試卷詳情

2023-2024學年廣東省四校聯考高三（上）期中數學試卷

發布：2024/10/7 3:0:2

一、單選題（本大題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的）.

1．已知集合A={x|lgx≤0}，B={x||x-1|≤1}，則A∩B=（　　）
A．A B．B C．?_RA D．?_RB
組卷：13引用：1難度：0.8
解析
2．已知向量
a
=（-3，m），
b
=（1，-2），若
b
∥
（
a
-
b
），則m的值為（　　）
A．-6 B．-4 C．0 D．6
組卷：149引用：4難度：0.8
解析
3．若函數f（x）=
a
x
-
3
，
x
≥
4
-
ax
+
4
，
x
＜
4
（a＞0，a≠1）是定義在R上的單調函數，則a的取值范圍為（　　）
A．
（
0
，
1
）
∪
（
1
，
5
4
]
B．
（
1
，
5
4
]
C．
（
0
，
4
5
]
D．
[
4
5
，
1
）
組卷：67引用：1難度：0.8
解析
4．若復數z滿足（1+i）z=|1+i|，則
z
的虛部為（　　）
A．
-
2
i
B．
-
2
2
C．
2
2
i
D．
2
2
組卷：64引用：1難度：0.7
解析
5．數列{a_n}滿足a₁=2019，且對?n∈N^*，恒有
a
n
+
3
=
a
n
+
2
n
，則a₇=（　　）
A．2021 B．2023 C．2035 D．2037
組卷：156引用：3難度：0.8
解析
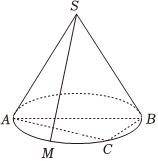6．如圖，已知圓錐的頂點為S，AB為底面圓的直徑，點M，C為底面圓周上的點，并將弧AB三等分，過AC作平面α，使SB∥α，設α與SM交于點N，則
SM
SN
的值為（　　）
A．
4
3
B．
3
2
C．
2
3
D．
3
4
組卷：228引用：5難度：0.6
解析
7．已知函數f（x）及其導函數f′（x）的定義域均為R，且f（x）為偶函數，
f
（
π
6
）
=
-
2
，3f（x）cosx+f'（x）sinx＞0，則不等式
f
（
x
+
π
2
）
co
s
3
x
+
1
2
＞
0
的解集為（　　）
A．
（
-
π
3
，
+
∞
）
B．
（
-
2
π
3
，
+
∞
）
C．
（
-
2
π
3
，
π
3
）
D．
（
π
3
，
+
∞
）
組卷：17引用：3難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（本大題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟）

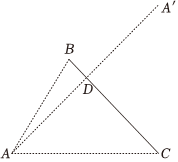21．某單位為端正工作人員儀容，在單位設置一面平面鏡．如圖，平面鏡寬BC為2m,某人在A點處觀察到自己在平面鏡中所成的像為A′．當且僅當線段AA′與線段BC有異于B，C的交點D時，此人能在鏡中看到自己的像．已知
∠
BAC
=
π
3
．
（1）若在A點處能在鏡中看到自己的像，求
AC
AB
的取值范圍；
（2）求某人在A處與其在平面鏡中的像的距離AA′的最大值．
組卷：19引用：2難度：0.4
解析
22．設f（x）=ax²+cosx-1，a∈R．
（1）當
a
=
1
π
時，求函數f（x）的最小值；
（2）當
a
≥
1
2
時．證明：f（x）≥0；
（3）證明：
cos
1
2
+
cos
1
3
+
?
+
cos
1
n
＞
n
-
4
3
（
n
∈
N
*
，
n
＞
1
）
．
組卷：345引用：7難度：0.2
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（ 0 ， 1 ） ∪ （ 1 ， 5 4 ]	B．（ 1 ， 5 4 ]
C．（ 0 ， 4 5 ]	D． [ 4 5 ， 1 ）

2023-2024學年廣東省四校聯考高三（上）期中數學試卷

一、單選題（本大題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的）.

1．已知集合A={x|lgx≤0}，B={x||x-1|≤1}，則A∩B=（ ）

2．已知向量a=（-3，m），b=（1，-2），若b∥（a-b），則m的值為（ ）

3．若函數f（x）=ax-3，x≥4-ax+4，x＜4（a＞0，a≠1）是定義在R上的單調函數，則a的取值范圍為（ ）

4．若復數z滿足（1+i）z=|1+i|，則z的虛部為（ ）

5．數列{an}滿足a1=2019，且對?n∈N*，恒有an+3=an+2n，則a7=（ ）

6．如圖，已知圓錐的頂點為S，AB為底面圓的直徑，點M，C為底面圓周上的點，并將弧AB三等分，過AC作平面α，使SB∥α，設α與SM交于點N，則SMSN的值為（ ）

7．已知函數f（x）及其導函數f′（x）的定義域均為R，且f（x）為偶函數，f（π6）=-2，3f（x）cosx+f'（x）sinx＞0，則不等式f（x+π2）cos3x+12＞0的解集為（ ）

四、解答題（本大題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟）

22．設f（x）=ax2+cosx-1，a∈R．（1）當a=1π時，求函數f（x）的最小值；（2）當a≥12時．證明：f（x）≥0；（3）證明：cos12+cos13+?+cos1n＞n-43（n∈N*，n＞1）．

1．已知集合A={x|lgx≤0}，B={x||x-1|≤1}，則A∩B=（　　）

2．已知向量
a
=（-3，m），
b
=（1，-2），若
b
∥
（
a
-
b
），則m的值為（　　）

3．若函數f（x）=
a
x
-
3
，
x
≥
4
-
ax
+
4
，
x
＜
4
（a＞0，a≠1）是定義在R上的單調函數，則a的取值范圍為（　　）

4．若復數z滿足（1+i）z=|1+i|，則
z
的虛部為（　　）

5．數列{a_n}滿足a₁=2019，且對?n∈N^*，恒有
a
n
+
3
=
a
n
+
2
n
，則a₇=（　　）

6．如圖，已知圓錐的頂點為S，AB為底面圓的直徑，點M，C為底面圓周上的點，并將弧AB三等分，過AC作平面α，使SB∥α，設α與SM交于點N，則
SM
SN
的值為（　　）

7．已知函數f（x）及其導函數f′（x）的定義域均為R，且f（x）為偶函數，
f
（
π
6
）
=
-
2
，3f（x）cosx+f'（x）sinx＞0，則不等式
f
（
x
+
π
2
）
co
s
3
x
+
1
2
＞
0
的解集為（　　）

22．設f（x）=ax²+cosx-1，a∈R．
（1）當
a
=
1
π
時，求函數f（x）的最小值；
（2）當
a
≥
1
2
時．證明：f（x）≥0；
（3）證明：
cos
1
2
+
cos
1
3
+
?
+
cos
1
n
＞
n
-
4
3
（
n
∈
N
*
，
n
＞
1
）
．