2020-2021學年四川省眉山市仁壽一中南校區高一（下）開學數學試卷

一、選擇題：本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知集合

  A

  =

  {

  x

  |

  -

  1

  ≤

  x

  ≤

  1

  }

  ，

  B

  =

  {

  x

  |

  2

  x

  ＞

  1

  2

  }

  ，則A∪B=（　　）

  A．[-1，+∞）

  B．[-1，1]

  C．（-1，+∞）

  D．（-1，1]
  組卷：64引用：3難度：0.8

  解析

• 2．已知角α的頂點在原點，始邊與x軸非負半軸重合，終邊與以原點為圓心，半徑為1的圓相交于點

  A

  （

  -

  3

  5

  ，

  4

  5

  ）

  ，則tanα=（　　）

  A． 3 4

  B． 4 3

  C． - 3 4

  D． - 4 3
  組卷：98引用：3難度：0.8

  解析

• 3．已知冪函數f（x）=x^α（α∈R）的圖象過點

  （

  4

  ，

  1

  2

  ）

  ，則α=（　　）

  A． - 1 4

  B． - 1 2

  C． 1 2

  D． 1 4
  組卷：230引用：3難度：0.8

  解析

• 4．方程2^x+x=4的根所在的區間為（　　）

  A．（0，1）

  B．（1，2）

  C．（2，3）

  D．（3，4）
  組卷：44引用：2難度：0.7

  解析

• 5．若

  sin

  （

  π

  3

  -

  α

  ）

  =

  -

  1

  3

  ，則

  cos

  （

  α

  +

  π

  6

  ）

  =（　　）

  A． - 1 3

  B． - 2 2 3

  C． 1 3

  D． 2 2 3
  組卷：34引用：2難度：0.7

  解析

• 6．若向量

  a

  =（1，5），

  b

  =（1，-1），則向量

  a

  +

  2

  b

  與

  b

  -

  a

  的夾角等于（　　）

  A． 3 π 4

  B． π 4

  C． π 6

  D． - π 4
  組卷：9引用：2難度：0.8

  解析

• 7．函數

  f

  （

  x

  ）

  =

  （

  1

  2

  ）

  |

  x

  -

  1

  |

  的圖像大致為（　　）

  A．

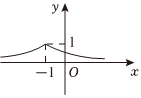
  B．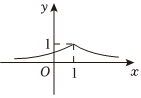

  C．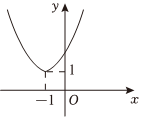

  D．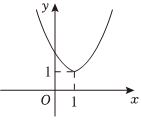
  組卷：10引用：1難度：0.7

  解析

三、解答題：本大題6個小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．已知f（x）是定義在R上的奇函數．當x＜0時，f（x）為二次函數且f（-3）=f（-1）=3，f（-4）=0．
  （1）求函數f（x）在R上的解析式；
  （2）若函數f（x）在區間[log₂m,2]上單調遞減，求實數m的取值范圍．
  組卷：140引用：3難度：0.7

  解析

• 22．對于函數f₁（x），f₂（x），如果存在實數a,b,使得f（x）=af₁（x）-bf₂（x），那么稱f（x）為f₁（x），f₂（x）的親子函數．
  （1）已知f₁（x）=2x-3，f₂（x）=x+1，試判斷f（x）=4x-11是否為f₁（x），f₂（x）的親子函數，若是，求出a,b；若不是，說明理由；
  （2）已知f₁（x）=3^x，f₂（x）=9^x，f（x）為f₁（x），f₂（x）的親子函數，且a=4，b=1．
  （i）若g（x）=（m+1）f₂（x）-f（x）+1，當-1≤x≤0時，g（x）≤0恒成立，求正數m的取值范圍；
  （ⅱ）若關于x的方程f（x）=nf₂（x）+1有實數解，求實數n的取值范圍．
  組卷：4引用：1難度：0.5

  解析