2021年廣東省廣州市南沙區中考數學二模試卷

一．選擇題（共10小題，每題3分，共30分）

• 1．2022^-1等于（　　）

  A．-2022

  B． 1 2022

  C． - 1 2022

  D．2022
  組卷：756引用：9難度：0.9

  解析

• 2．北京2022年冬奧會一共有超過1.9萬名賽會志愿者，還有20余萬人次的城市志愿者，他們是溫暖這個冬天的雪花，他們把自己的志愿化成一道冬日的光，凝聚成溫暖世界的力量．將20萬用科學記數法表示應為（　　）

  A．20×104

  B．2×104

  C．2×105

  D．0.2×106
  組卷：139引用：4難度：0.8

  解析

• 3．下列算式中，計算正確的是（　　）

  A． （ - 3 ） 2 =-3	B．|3-π|=3-π
  C．（-3ab）2=6a2b2	D．3-3= 1 27
  組卷：232引用：2難度：0.6

  解析

• 4．已知2a+1和5是正數b的兩個不同平方根，則a+b的值是（　　）

  A．25

  B．30

  C．20

  D．22
  組卷：1270引用：5難度：0.6

  解析

• 5．如圖，在矩形ABCD中，對角線AC與BD相交于點O，已知∠ACB=25°，則∠AOB的大小是（　　）

  A．130°

  B．65°

  C．50°

  D．25°
  組卷：2343引用：24難度：0.5

  解析

• 6．若一次函數y=ax+b的圖象經過第一、二、四象限，則

  a

  2

  -

  （

  b

  -

  a

  ）

  2

  =（　　）

  A．-2a-b

  B．2a-b

  C．-b

  D．-2a+b
  組卷：962引用：7難度：0.6

  解析

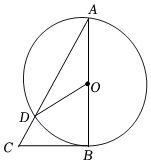• 7．如圖，AB是⊙O的直徑，BC是⊙O的切線，點B為切點，若BC=4cm,tan∠BAC=

  3

  3

  ，則劣弧BD的長為（　　）

  A． 3 π 3 cm

  B． 3 π 2 cm

  C． 2 3 π 3 cm

  D． 3 πcm
  組卷：493引用：6難度：0.8

  解析

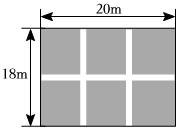• 8．如圖，某校勞動實踐課程試驗園地是長為20m,寬為18m的矩形，為方便活動，需要在園地中間開辟一橫兩縱共三條等寬的小道．如果園地余下的面積為306m²，則小道的寬為多少？設小道的寬為x m,根據題意，可列方程為（　　）

  A．（20-2x）（18-x）=306

  B．（20-x）（18-2x）=306

  C．20×18-2×18x-20x+x2=306

  D．20×18-2×20x-18x+x2=306
  組卷：995引用：7難度：0.7

  解析

三、解答題（本大題共9小題，滿分0分，解答應寫出文字說明、證明過程或演算步驟）

• 24．已知拋物線y=x²+6mx+9m²-6m-8的頂點為P．
  （1）當m=1時，求點P的坐標；
  （2）經過探究發現，隨著m的變化，頂點P在某直線l上運動，直線l與x軸，y軸分別交于A，B兩點，求△AOB的面積；
  （3）若拋物線與直線l的另一交點為Q，以PQ為直徑的圓與坐標軸相切，求m的值．
  組卷：1100引用：4難度：0.2

  解析

• 25．如圖1，在平面直角坐標系xOy中，點A的坐標為（5，0），點B在第一象限內，且使得AB=4，OB=3．
  （1）試判斷△AOB的形狀，并說明理由；
  （2）在第二象限內是否存在一點P，使得△POB是以OB為腰的等腰直角三角形，若存在，求出點P的坐標；若不存在，請說明理由；
  （3）如圖2，點C為線段OB上一動點，點D為線段BA上一動點，且始終滿足OC=BD．求AC+OD的最小值．
  
  組卷：1939引用：11難度：0.2

  解析