2023年河南省漯河高中高考數(shù)學(xué)適應(yīng)性試卷（文科）

一、選擇題（本題共12小題，每小題5分，共60分.題只有一項符合要求.）

• 1．已知集合A=[-2，5]，B=[m+1，2m-1]．若“x∈B”是“x∈A”的充分不必要條件，則m的取值范圍是（　　）

  A．（-∞，3]

  B．（2，3]

  C．?

  D．[2，3]
  組卷：248引用：4難度：0.7

  解析

• 2．若復(fù)數(shù)z是方程x²-2x+2=0的一個根，則i?z的虛部為（　　）

  A．2

  B．2i

  C．i

  D．1
  組卷：106引用：2難度：0.8

  解析

• 3．“cosθ=0”是“函數(shù)f（x）=sin（x+θ）+cosx為偶函數(shù)”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：625引用：6難度：0.8

  解析

• 4．若如圖所示的程序框圖輸出的結(jié)果為S=720，則圖中空白框中應(yīng)填入（　　）
  

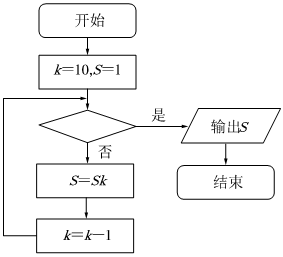
  A．k≤7？

  B．k＞7？

  C．k≤8？

  D．k＞8？
  組卷：49引用：3難度：0.8

  解析

• 5．已知首項為

  1

  2

  的數(shù)列{a_n}的前n項和為S_n，若（S_n+1-S_n）（a_n+1）+1=a_n，則a₁?a₂?a₃……a₂₀₂₃=（　　）

  A． 1 2

  B．1

  C． - 1 6

  D． 1 3
  組卷：52引用：2難度：0.7

  解析

• 6．已知函數(shù)f（x）=2sin（ωx+φ）（ω＞0，0＜φ＜

  π

  2

  ）．若f（x-

  π

  3

  ）為偶函數(shù)，

  f

  （

  x

  +

  π

  3

  ）

  為奇函數(shù)，則ω的值可以是（　　）

  A． 3 4

  B． 5 4

  C． 7 4

  D． 9 4
  組卷：111引用：1難度：0.7

  解析

• 7．阿基米德在他的著作《關(guān)于圓錐體和球體》中計算了一個橢圓的面積．當(dāng)我們垂直地縮小一個圓時，我們得到一個橢圓．橢圓的面積等于圓周率π與橢圓的長半軸長與短半軸長的乘積．已知橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的面積為21π，點P在橢圓C上，且點P與橢圓C左、右頂點連線的斜率之積為

  -

  9

  49

  ，記橢圓C的兩個焦點分別為F₁，F(xiàn)₂，則|PF₁|的值不可能為（　　）

  A．4

  B．7

  C．10

  D．14
  組卷：72引用：2難度：0.6

  解析

三、解答題（共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟.）

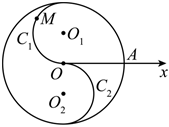• 22．如圖，在極坐標(biāo)系Ox中，圓O的半徑為2，半徑均為1的兩個半圓弧C₁，C₂所在圓的圓心分別為

  O

  1

  （

  1

  ，

  π

  2

  ）

  ，

  O

  2

  （

  1

  ，

  3

  π

  2

  ）

  ，M是半圓弧C₁上的一個動點．
  （1）若點A是圓O與極軸的交點，求|MA|的最大值；
  （2）若點N是射線

  θ

  =

  π

  4

  ，

  （

  ρ

  ≥

  0

  ）

  與圓O的交點，求△MON面積的取值范圍．
  組卷：153引用：9難度：0.4

  解析

• 23．已知函數(shù)f（x）=|x-a|+|x-b|．
  （1）若|a-b|＞c,解不等式f（x）＞c；
  （2）若b=1，且不等式f（x）＜2-|a-2|的解集非空，求a的取值范圍．
  組卷：52引用：4難度：0.5

  解析