2022-2023學年浙江省湖州市安吉高級中學高三（上）期末數學試卷

一、單項選擇題：本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合

  A

  =

  {

  x

  |

  x

  2

  -

  x

  -

  6

  ≤

  0

  }

  ，

  B

  =

  {

  x

  |

  x

  -

  4

  x

  +

  1

  ≤

  0

  }

  ，則A∩B=（　　）

  A．{x|-1＜x≤3}

  B．{x|x≤3或x＞4}

  C．{x|-2≤x≤4}

  D．{x|-2≤x≤-1}
  組卷：174引用：2難度：0.7

  解析

• 2．設復數z滿足

  z

  =

  4

  +

  2

  i

  （其中i為虛數單位），則

  z

  4

  +

  2

  i

  =（　　）

  A． 3 - 4 i 3

  B． 3 + 4 i 3

  C． 3 - 4 i 5

  D． 3 + 4 i 5
  組卷：140引用：2難度：0.7

  解析

• 3．設坐標原點為O，拋物線y²=4x的焦點為F，過點F的直線交該拋物線于A，B兩點，則

  OA

  ?

  OB

  =（　　）

  A． 3 4

  B． - 3 4

  C．3

  D．-3
  組卷：104引用：2難度：0.5

  解析

• 4．已知

  α

  ∈

  （

  0

  ，

  π

  2

  ）

  ，2sin2α=cos2α+1，則

  cos

  （

  3

  π

  2

  +

  α

  ）

  =（　　）

  A． 1 5

  B． 5 5

  C． 2 5 5

  D． - 5 5
  組卷：229引用：5難度：0.7

  解析

• 5．已知正方形ABCD的邊長為2，MN是它的內切圓的一條弦，點P為正方形四條邊上的動點，當弦MN的長度最大時，

  PM

  ?

  PN

  的取值范圍是（　　）

  A．[0，1]

  B． [ 0 ， 2 ]

  C．[1，2]

  D．[-1，1]
  組卷：713引用：6難度：0.5

  解析

• 6．研究變量x,y得到一組樣本數據，進行回歸分析，以下說法中錯誤的是（　　）

  A．若變量x和y之間的相關系數為r=-0.992，則變量x和y之間的負相關很強

  B．用決定系數R2來比較兩個模型擬合效果，R2越大，表示殘差平方和越小，即模型的擬合效果越好

  C．在經驗回歸方程 ? y = - 2 x + 0 . 8 中，當解釋變量x每增加1個單位時，響應變量 ? y 平均減少2個單位

  D．經驗回歸直線 y = ? b x + ? a 至少經過點（x1，y1），（x2，y2），…，（xn，yn）中的一個
  組卷：266引用：5難度：0.7

  解析

• 7．已知

  a

  =

  e

  sin

  1

  +

  1

  e

  sin

  1

  ，

  b

  =

  e

  tan

  2

  +

  1

  e

  tan

  2

  ，

  c

  =

  e

  cos

  3

  +

  1

  e

  cos

  3

  ，則（　　）

  A．a＞b＞c

  B．a＞c＞b

  C．b＞c＞a

  D．c＞a＞b
  組卷：391引用：8難度：0.5

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

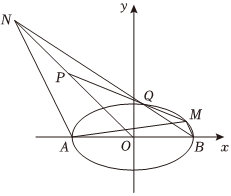• 21．如圖所示，A，B為橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左、右頂點，離心率為

  3

  2

  ，且經過點

  （

  3

  ，

  1

  2

  ）

  ．
  （1）求橢圓C的方程；
  （2）已知O為坐標原點，點P（-2，2），點M是橢圓C上的點，直線PM交橢圓C于點Q（M，Q不重合），直線BQ與OP交于點N．求證：直線AM，AN的斜率之積為定值，并求出該定值．
  組卷：210引用：6難度：0.5

  解析

• 22．已知a＞0且a≠1，函數

  f

  （

  x

  ）

  =

  lo

  g

  a

  x

  +

  1

  2

  a

  x

  2

  ．
  （1）若a=e,求函數f（x）在x=1處的切線方程；
  （2）若函數f（x）有兩個零點，求實數a的取值范圍．
  組卷：215引用：5難度：0.2

  解析